题目内容
设椭圆C1的方程为
=1(a＞b＞0)，曲线C2的方程为y=
，且C1与C2在第一象限内只有一个公共点P.(Ⅰ)试用a表示点P的坐标.
(Ⅱ)设A、B是椭圆C1的两个焦点，当a变化时，求△ABP的面积函数S(a)的值域；
(Ⅲ)设min｛y1，y2，…，yn｝为y1，y2，…，yn中最小的一个设g(a)是以椭圆C1的半焦距为边长的正方形的面积，试函数f(a)=min｛g(a),S(a)｝的表达式.
(Ⅰ)解：将y=代入椭圆方程，得=1，
化简得b2x4－a2b2x2+a2=0，
由条件，有Δ=a4b4－4a2b2=0,得ab=2
解得x=
,x=－
(舍去)
故P的坐标为(
,
)
(Ⅱ)解：∵在ΔABP中,｜AB｜=2
，高为
，
∴S(a)=
·2
·
=2
∵a＞b＞0，b=
，
∴a＞
,
即a＞
，得0＜
＜1，
于是0＜S(a)＜2故ΔABP的面积函数S(a)的值域为(0，
)
(Ⅲ)解：g(a)=c2=a2－b2=a2－
，
解不等式：g(a)≥S(a)，
即a2－
≥
，
整理得：a8－10a4+24≥0，
即(a4－4)(a4－6)≥0，
即(a4－4)(a4－6)≥0
解得：a≤2(舍去)或a≥
,
故f(a)=min｛g(a),S(a)｝=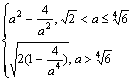
练习册系列答案
相关题目
=1（a＞b＞0），曲线C2的方程为y=
，且C1与C2在第一象限内只有一个公共点P.
(a＞b＞0)，曲线C2的方程为y=
，且曲线C1与C2在第一象限内只有一个公共点P.
(a＞b＞0)，曲线C2的方程为y=
，且曲线C1与C2在第一象限内只有一个公共点P。（1）试用a表示点P的坐标；（2）设A、B是椭圆C1的两个焦点，当a变化时，求△ABP的面积函数S(a)的值域；（3）记min{y1,y2,……,yn}为y1,y2,……,yn中最小的一个。设g(a)是以椭圆C1的半焦距为边长的正方形的面积，试求函数f(a)=min{g(a), S(a)}的表达式。
=1(a＞b＞0)，曲线C2的方程为y=
，且C1与C2在第一象限内只有一个公共点P.