题目内容
已知三个平面α、β、γ,且α∥γ,β∥γ.
求证:α∥β.
解法一:如图,在α内作两相交直线a、b,且过α作平面M与γ交于a′,再过a′作平面N交平面β于a″.∵α∥γ,M∩γ=a′,
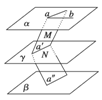
N∩β=a″,∴a∥a′,同理a″∥a′,∴a∥a″,
又a⊄β(否则α与β重合)
∴a∥β,同理b∥β,
又a、b是α内两条相交直线,∴α∥β.
解法二:假设αβ,则α与β有公共点,设公共点为P,由已知α∥γ,β∥γ,得知过点P有两个平面α、β都与γ平行.这与“经过平面外一点有且只有一个平面和已知平面平行”矛盾,从而得证.

练习册系列答案
相关题目