题目内容
【题目】辽宁省六校协作体（葫芦岛第一高中、东港二中、凤城一中、北镇高中、瓦房店高中、丹东四中）中的某校文科实验班的
名学生期中考试的语文、数学成绩都不低于分，其中语文成绩的频率分布直方图如图所示，成绩分组区间是：
、
、
、
、
．
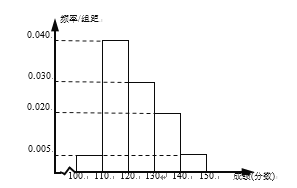
（1）根据频率分布直方图，估计这名学生语文成绩的中位数和平均数；（同一组数据用该区间的中点值作代表；中位数精确到
）
（2）若这名学生语文成绩某些分数段的人数
与数学成绩相应分数段的人数
之比如下表所示：
分组区间 |
|
|
|
|
|
|
|
|
|
从数学成绩在
的学生中随机选取
人，求选出的人中恰好有
人数学成绩在的概率．
【答案】（1）中位数是
；平均数是
；（2）
.
【解析】
（1）利用中位数左边矩形面积之和为
可求出中位数，将每个矩形底边中点值乘以相应矩形的面积，再相加可得出这
名学生语文成绩的平均数；
（2）计算出数学成绩在
、
的学生人数，列举出所有的基本事件，然后利用古典概型的概率公式可计算出所求事件的概率.
（1）
，
，
这名学生语文成绩的中位数是
.
这名学生语文成绩的平均数是：
；
（2）
数学成绩在
之内的人数为
，
数学成绩在的人数为
人，设为
、
、
，
而数学成绩在
的人数为
人，设为
、
，
从数学成绩在的学生中随机选取
人基本事件为：
、
、
、
、
、
、
、
、
、
，共
个，
选出的人中恰好有
人数学成绩在的基本事件为：
、、、、、，共
个，
选出的人中恰好有人数学成绩在的概率是．
【题目】为更好地落实农民工工资保证金制度，南方某市劳动保障部门调查了2018年下半年该市
名农民工(其中技术工、非技术工各
名)的月工资，得到这名农民工的月工资均在
(百元)内，且月工资收入在
(百元)内的人数为
，并根据调查结果画出如图所示的频率分布直方图:
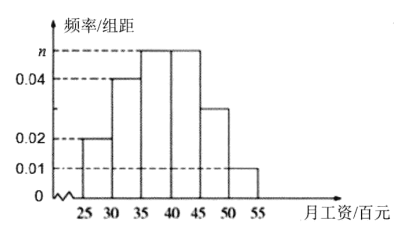
(1)求
的值；
(2)已知这名农民工中月工资高于平均数的技术工有
名，非技术工有
名.
①完成如下所示
列联表
技术工 | 非技术工 | 总计 | |
月工资不高于平均数 |
| ||
月工资高于平均数 |
| ||
总计 |
|
|
|
②则能否在犯错误的概率不超过
的前提下认为是不是技术工与月工资是否高于平均数有关系?
参考公式及数据: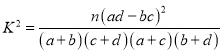
，其中
.
|
|
|
|
|
|
|
|
|
|
【题目】辽宁省六校协作体（葫芦岛第一高中、东港二中、凤城一中、北镇高中、瓦房店高中、丹东四中）中的某校理科实验班的100名学生期中考试的语文、数学成绩都不低于100分，其中语文成绩的频率分布直方图如图所示，成绩分组区间是：[100,110），[110,120），[120,130），[130,140），[140,150]．
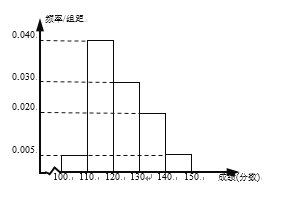
这100名学生语文成绩某些分数段的人数
与数学成绩相应分数段的人数
之比如下表所示：
分组区间 | [100,110） | [110,120） | [120,130） | [130,140） |
| 1:2 | 2:1 | 3:4 | 1:1 |
（1）估计这100名学生语文成绩的平均数、方差（同一组数据用该区间的中点值作代表）；
（2）从数学成绩在[130，150] 的学生中随机选取2人，该2人中数学成绩在[140，150]的人数为
，求的数学期望
．
