题目内容
已知平面上三个向量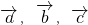 ,其中
,其中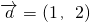 ,
,
(1)若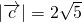 ,且
,且 ∥
∥ ,求
,求 的坐标;
的坐标;
(2)若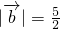 ,且
,且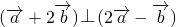 ,求
,求 与
与 夹角的余弦值.
夹角的余弦值.
解:(1)设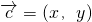 ,由条件有
,由条件有 ,
,
解得: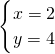 ,或
,或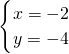 ,
,
所以: ,或
,或 .
.
(2)设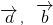 的夹角为θ,由
的夹角为θ,由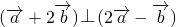 ,
,
知 ,
,
即: ,
,
由于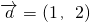 ?
? ,
,
∴ ,又
,又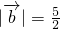 ,
,
所以: ,
,
又 .
.
分析:(1)设出 的坐标,利用它与
的坐标,利用它与 平行以及它的模等于2
平行以及它的模等于2 ,利用待定系数法求出
,利用待定系数法求出 的坐标.
的坐标.
(2)由 +2
+2 与2
与2 -
- 垂直,数量积等于0,求出夹角θ的余弦值的大小.
垂直,数量积等于0,求出夹角θ的余弦值的大小.
点评:本题考查平面上两个向量平行、垂直的条件,以及利用两个向量的数量积求两个向量的夹角.属于基础题.
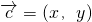 ,由条件有
,由条件有 ,
,解得:
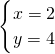 ,或
,或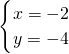 ,
,所以:
 ,或
,或 .
.(2)设
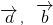 的夹角为θ,由
的夹角为θ,由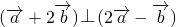 ,
,知
 ,
,即:
 ,
,由于
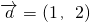 ?
? ,
,∴
 ,又
,又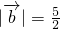 ,
,所以:
 ,
,又
 .
.分析:(1)设出
 的坐标,利用它与
的坐标,利用它与 平行以及它的模等于2
平行以及它的模等于2 ,利用待定系数法求出
,利用待定系数法求出 的坐标.
的坐标.(2)由
 +2
+2 与2
与2 -
- 垂直,数量积等于0,求出夹角θ的余弦值的大小.
垂直,数量积等于0,求出夹角θ的余弦值的大小.点评:本题考查平面上两个向量平行、垂直的条件,以及利用两个向量的数量积求两个向量的夹角.属于基础题.

练习册系列答案
相关题目
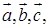 的模均为1,它们相互之间的夹角均为
的模均为1,它们相互之间的夹角均为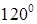 。
。 ;
;
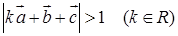 ,求
,求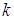 的取值范围。
的取值范围。