Question

在四棱锥P-ABCD中，底面ABCD是平行四边形，PD⊥平面ABCD，PA⊥CD，且；
（1）求证：CD⊥AD；
（2）求二面角A-PB-C的正弦值；
（3）若E，F，M为AB，CD，PB的中点，在线段EF上是否存在点N，使得MN⊥平面PAB；若存在，求出点N的位置；若不存在，请说明理由．

Answer 1

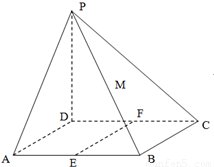
【答案】分析：（1）由PD⊥平面ABCD，知PD⊥CD，由PA⊥CD，能够证明CD⊥AD．
（2）以DA为x轴，DC为y轴，DP为z轴，建立空间直角坐标系，利用向量法能求出二面角A-PB-C的正弦值．
（3）假设存在．由E，F，M为AB，CD，PB的中点，设，利用向量法能求出．
解答：解：（1）∵PD⊥平面ABCD，∴PD⊥CD，
又∵PA⊥CD，∴CD⊥平面PAD，
∴CD⊥AD．
（2）如图，以DA为x轴，DC为y轴，DP为z轴，建立空间直角坐标系，
∵ABCD是平行四边形，CD⊥AD，，
则D（0，0，0），A（3，0，0），B（3，2，0），C（0，2，0），P（0，0，3），
=（0，2，0），=（3，2，-3），=（3，0，0），
设平面APB的法向量=（x₁，y₁，z₁），则，=0，
∴，解得=（1，0，），
设平面CPB的法向量=（x₂，y₂，z₂），则，，
∴，解得=（0，3，2），
设二面角A-PB-C的平面角为θ，
则cosθ=|cos＜＞|=||=，
∴二面角A-PB-C的正弦值为：=．
（3）假设存在．
∵E，F，M为AB，CD，PB的中点，
∴E（3，，0），F（0，，0），=（3，0，0），
设，M（），=（），，
∵MN⊥平面PAB，
∴，
∴．
故在线段EF上存在点N，FN=FE，使得MN⊥平面PAB．
点评：本题考查异面直线垂直的证明，考查直线与平面所成角的正弦值的求法，考查点的位置的探索．解题时要认真审题，仔细解答，注意向量法的合理运用．