题目内容
若函数f(x)的零点与g(x)=4x+2x-2的零点之差的绝对值不超过0.25,则f(x)可以是( )A.f(x)=4x-1
B.f(x)=(x-1)2
C.f(x)=ex-1
D.f(x)=ln(x-
 )
)
【答案】分析:先判断g(x)的零点所在的区间,再求出各个选项中函数的零点,看哪一个能满足与g(x)=4x+2x-2的零点之差的
绝对值不超过0.25.
解答:解:∵g(x)=4x+2x-2在R上连续,且g( )=
)=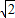 +
+ -2=
-2=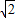 -
- <0,g(
<0,g( )=2+1-2=1>0.
)=2+1-2=1>0.
设g(x)=4x+2x-2的零点为x,则 <x<
<x< ,
,
0<x- <
< ,∴|x-
,∴|x- |<
|< .
.
又f(x)=4x-1零点为x= ;f(x)=(x-1)2零点为x=1;
;f(x)=(x-1)2零点为x=1;
f(x)=ex-1零点为x=0;f(x)=ln(x- )零点为x=
)零点为x= ,
,
故选A.
点评:本题考查判断函数零点所在的区间以及求函数零点的方法,属于基础题.
绝对值不超过0.25.
解答:解:∵g(x)=4x+2x-2在R上连续,且g(
 )=
)=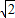 +
+ -2=
-2=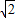 -
- <0,g(
<0,g( )=2+1-2=1>0.
)=2+1-2=1>0.设g(x)=4x+2x-2的零点为x,则
 <x<
<x< ,
,0<x-
 <
< ,∴|x-
,∴|x- |<
|< .
.又f(x)=4x-1零点为x=
 ;f(x)=(x-1)2零点为x=1;
;f(x)=(x-1)2零点为x=1;f(x)=ex-1零点为x=0;f(x)=ln(x-
 )零点为x=
)零点为x= ,
,故选A.
点评:本题考查判断函数零点所在的区间以及求函数零点的方法,属于基础题.

练习册系列答案
相关题目
若函数f(x)的零点与g(x)=4x+2x-2的零点之差的绝对值不超过0.25,则f(x)可以是( )
| A、f(x)=4x-1 | ||
| B、f(x)=(x-1)2 | ||
| C、f(x)=ex-1 | ||
D、f(x)=ln(x-
|