题目内容
(难应用举例)已知向量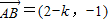 ,
, .
.(1)若△ABC为直角三角形,求k值;
(2)若△ABC为等腰直角三角形,求k值.
【答案】分析:(1)先表示出向量 ,对A、B、C分别为直角进行讨论即可.
,对A、B、C分别为直角进行讨论即可.
(2)对(1)中解出的k的值进行讨论,分别验证是否为等腰三角形.
解答:解:(1) ,
,
①若∠A=90°,则
 (2-k,-1)•(1,k)=0,∴k=1;
(2-k,-1)•(1,k)=0,∴k=1;
②若∠B=90°,则
 (2-k,-1)•(k-1,k+1)=0,得k2-2k+3=0无解;
(2-k,-1)•(k-1,k+1)=0,得k2-2k+3=0无解;
③若∠C=90°,则
 (1,k)•(k-1,k+1)=0,得k2+2k-1=0,
(1,k)•(k-1,k+1)=0,得k2+2k-1=0,
∴ .
.
综上所述,当k=1时,△ABC是以A为直角顶点的直角三角形;
当 时,△ABC是以C为直角顶点的直角三角形.
时,△ABC是以C为直角顶点的直角三角形.
(2)①当k=1时, ,
,
 =
= ;
;
②当 时,
时, ,
, =
= ,
,
得 ,
, ,
,
 ;
;
③当 时,
时, ,
, =
= ,
,
得 ,
, ,
,
 ;
;
综上所述,当k=1时,△ABC是以BC为斜边的等腰直角三角形.
点评:本题主要考查向量垂直和点乘之间的关系,即两向量互相垂直则二者点乘为0.
 ,对A、B、C分别为直角进行讨论即可.
,对A、B、C分别为直角进行讨论即可.(2)对(1)中解出的k的值进行讨论,分别验证是否为等腰三角形.
解答:解:(1)
 ,
,
①若∠A=90°,则

 (2-k,-1)•(1,k)=0,∴k=1;
(2-k,-1)•(1,k)=0,∴k=1;②若∠B=90°,则

 (2-k,-1)•(k-1,k+1)=0,得k2-2k+3=0无解;
(2-k,-1)•(k-1,k+1)=0,得k2-2k+3=0无解;③若∠C=90°,则

 (1,k)•(k-1,k+1)=0,得k2+2k-1=0,
(1,k)•(k-1,k+1)=0,得k2+2k-1=0,∴
 .
.综上所述,当k=1时,△ABC是以A为直角顶点的直角三角形;
当
 时,△ABC是以C为直角顶点的直角三角形.
时,△ABC是以C为直角顶点的直角三角形.(2)①当k=1时,
 ,
,
 =
= ;
;②当
 时,
时, ,
, =
= ,
,得
 ,
, ,
,
 ;
;③当
 时,
时, ,
, =
= ,
,得
 ,
, ,
,
 ;
;综上所述,当k=1时,△ABC是以BC为斜边的等腰直角三角形.
点评:本题主要考查向量垂直和点乘之间的关系,即两向量互相垂直则二者点乘为0.

练习册系列答案
相关题目
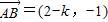 ,
,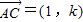 .
.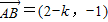 ,
,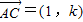 .
.