题目内容
已知函数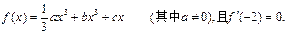
(1)若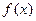 在x=2处取得极小值-2,求
在x=2处取得极小值-2,求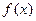 的单调区间;
的单调区间;
(2)令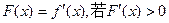 的解集是A,且A∪(0,1)=(-∞,1),求
的解集是A,且A∪(0,1)=(-∞,1),求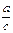 的最大值.
的最大值.
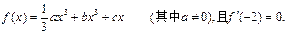
(1)若
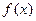 在x=2处取得极小值-2,求
在x=2处取得极小值-2,求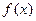 的单调区间;
的单调区间;(2)令
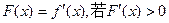 的解集是A,且A∪(0,1)=(-∞,1),求
的解集是A,且A∪(0,1)=(-∞,1),求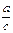 的最大值.
的最大值.(1)函数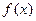 的单调减区间是[-2,2],增区间是
的单调减区间是[-2,2],增区间是
(2)
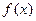 的单调减区间是[-2,2],增区间是
的单调减区间是[-2,2],增区间是
(2)

(1)


即函数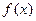 的单调减区间是[-2,2],增区间是
的单调减区间是[-2,2],增区间是 (2)
(2)

当a>0时,
当a<0时,
若满足




即函数
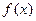 的单调减区间是[-2,2],增区间是
的单调减区间是[-2,2],增区间是 (2)
(2)

当a>0时,

当a<0时,

若满足



练习册系列答案
相关题目
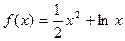 (1)求函数
(1)求函数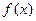 在区间[1,
在区间[1,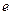 ]上的最大值、最小值;
]上的最大值、最小值;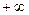 )上,函数
)上,函数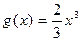 图象的下方;
图象的下方;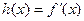 ,求证:
,求证: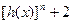 ≥
≥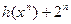 。(
。(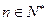 )
)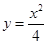 在点P(2, 1)处的切线方程为__________________________.
在点P(2, 1)处的切线方程为__________________________. 的斜率等于4的切线方程.
的斜率等于4的切线方程.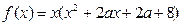 有三个零点
有三个零点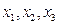 ,且
,且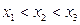 .
. 的取值范围;
的取值范围;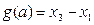 ,求函数
,求函数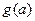 的值域.
的值域.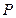 与周次
与周次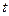 之间的函数关系;
之间的函数关系;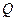 与周次
与周次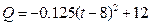 ,
,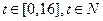 ,问该服装第几周每件销售利润最大?
,问该服装第几周每件销售利润最大?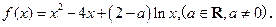
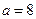 时,求函数
时,求函数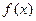 的单调区间;
的单调区间;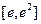 上的最小值.
上的最小值. ,
, .
. 的奇偶性并加以证明;
的奇偶性并加以证明; 时,解关于m的不等式
时,解关于m的不等式 .
. 求此物体在
求此物体在 和
和 时的瞬时速度.
时的瞬时速度.