题目内容
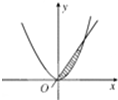
 如图,函数y=x2与y=kx(k>0)的图象所围成的阴影部分的面积为
如图,函数y=x2与y=kx(k>0)的图象所围成的阴影部分的面积为| 9 | 2 |
3
3
.分析:先联立两个解析式解方程,得到积分区间,然后利用积分的方法表示出阴影部分面积让其等于
,列出关于k的方程,求出解即可得到k的值.
| 9 |
| 2 |
解答:解:直线方程与抛物线方程联立
解得x=0,x=k,得到积分区间为[0,k],
由题意得:
∫0k(kx-x2)dx=(
x2-
x3)|0k=
-
=
=
,
即k3=27,解得k=3.
故答案为:3
|
解得x=0,x=k,得到积分区间为[0,k],
由题意得:
∫0k(kx-x2)dx=(
| k |
| 2 |
| 1 |
| 3 |
| k3 |
| 2 |
| k3 |
| 3 |
| k3 |
| 6 |
| 9 |
| 2 |
即k3=27,解得k=3.
故答案为:3
点评:此题是一道基础题,要求学生会利用积分求平面图形的面积.

练习册系列答案
相关题目
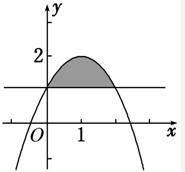 如图,函数y=-x2+2x+1与y=1相交形成一个闭合图形(图中的阴影部分),则该闭合图形的面积是( )
如图,函数y=-x2+2x+1与y=1相交形成一个闭合图形(图中的阴影部分),则该闭合图形的面积是( )| A、1 | ||
B、
| ||
C、
| ||
| D、2 |
 ,则k= .
,则k= .