题目内容
如图, 和
和 所在平面互相垂直,且
所在平面互相垂直,且 ,
, ,E、F、G分别为AC、DC、AD的中点.
,E、F、G分别为AC、DC、AD的中点.
(1)求证: 平面BCG;
平面BCG;
(2)求三棱锥D-BCG的体积.
附:椎体的体积公式 ,其中S为底面面积,h为高.
,其中S为底面面积,h为高.

 和
和 所在平面互相垂直,且
所在平面互相垂直,且 ,
, ,E、F、G分别为AC、DC、AD的中点.
,E、F、G分别为AC、DC、AD的中点.(1)求证:
 平面BCG;
平面BCG;(2)求三棱锥D-BCG的体积.
附:椎体的体积公式
 ,其中S为底面面积,h为高.
,其中S为底面面积,h为高.
(1)详见解析;(2)

试题分析:(1)由已知得,
 是
是 的中位线,故
的中位线,故 ,则可转化为证明
,则可转化为证明 平面BCG.易证
平面BCG.易证 ,则有
,则有 ,则在等腰三角形
,则在等腰三角形 和等腰三角形
和等腰三角形 中,且
中,且 是
是 中点,故
中点,故 ,
, .从而
.从而 平面BCG,进而
平面BCG,进而 平面BCG;(2)求四面体体积,为了便于计算底面积和高,往往可采取等体积转化法.由平面
平面BCG;(2)求四面体体积,为了便于计算底面积和高,往往可采取等体积转化法.由平面 平面
平面 ,利用面面垂直的性质,易作出面
,利用面面垂直的性质,易作出面 的垂线,同时求出点
的垂线,同时求出点 到面
到面 的距离,从而可求出点
的距离,从而可求出点 到平面
到平面 距离,即四面体
距离,即四面体 的高,进而求四面体体积.
的高,进而求四面体体积.(1)证明:由已知得
 .因此
.因此 .又
.又 为
为 中点,所以
中点,所以 ;同理
;同理 ;因此
;因此 平面
平面 .又
.又 .所以
.所以 平面BCG.
平面BCG.(2)在平面
 内.作
内.作 .交
.交 延长线于
延长线于 .由平面
.由平面 平面
平面 .知
.知 平面
平面 .
.又
 为
为 中点,因此
中点,因此 到平面
到平面 距离
距离 是
是 长度的一半.在
长度的一半.在 中,
中, .
.所以
 .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 .
. 时,求三棱锥F-DEG的体积V.
时,求三棱锥F-DEG的体积V.


 为正方形,四边形
为正方形,四边形 为等腰梯形,
为等腰梯形, ∥
∥ ,
, ,
, ,
, .
. 平面
平面 ;
; 与平面
与平面 所成角的正弦值.
所成角的正弦值.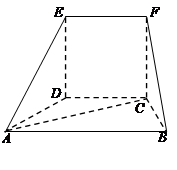

 ;
; ;
; .
. 为
为 ,
, ,
, ,A为垂足,
,A为垂足, ,
, ,
, ,则异面直线
,则异面直线 与
与 所成角的余弦值为
所成角的余弦值为


