题目内容
定义在R上的偶函数f(x)满足:对任意的x1,x2∈[0,+∞)(x1≠x2),有
<0,则( )
| A.f(3)<f(-2)<f(1) | B.f(1)<f(-2)<f(3) |
| C.f(-2)<f(1)<f(3) | D.f(3)<f(1)<f(-2) |
A
解析试题分析:∵函数f(x)是在[0,+∞)上单调递减的偶函数,∴f(3)<f(-2)=f(2)<f(1),故选A
考点:本题考查了单调性的运用
点评:对于抽象函数值比较大小问题,往往利用奇偶性把自变量转化为同一个单调区间上处理,解题的关键是判断抽象函数的单调性

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数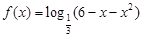 的单调递增区间是
的单调递增区间是
A. | B. | C. | D. |
若定义 上的函数
上的函数 满足:对于任意
满足:对于任意

 且当
且当 时有
时有 ,若
,若 的最大值、最小值分别为M,N,M+N等于( )
的最大值、最小值分别为M,N,M+N等于( )
| A.2011 | B.2012 | C.4022 | D.4024 |
已知函数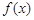 满足:①定义域为R;②
满足:①定义域为R;② ,有
,有 ;③当
;③当 时,
时, .记
.记 .根据以上信息,可以得到函数
.根据以上信息,可以得到函数 的零点个数为 ( )
的零点个数为 ( )
| A.15 | B.10 |
| C.9 | D.8 |
 的值属于区间
的值属于区间
A. | B. | C. | D. |
设函数 的定义域为
的定义域为 ,
,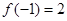 ,对于任意的
,对于任意的 ,
, ,则不等式
,则不等式 的解集为( )
的解集为( )
A. | B. |
C. | D. |
函数 的零点所在的一个区间是
的零点所在的一个区间是
A. | B. | C. | D. |
已知函数 的零点分别为
的零点分别为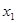 ,
, ,则( )
,则( )
A. | B. |
C. | D. |
 其中P,M为实数集R的两个非空子集,又规定f(P)={y|y=f(x),x∈P},f(M)={y|y=f(x),x∈M}.给出下列四个判断:①若P∩M=
其中P,M为实数集R的两个非空子集,又规定f(P)={y|y=f(x),x∈P},f(M)={y|y=f(x),x∈M}.给出下列四个判断:①若P∩M=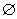 ,则f(P)∩f(M)=
,则f(P)∩f(M)=