题目内容
(本小题13分)已知二次函数![]() (其中
(其中![]() )
)
(1)试讨论函数![]() 的奇偶性.
的奇偶性.
(2)当![]() 为偶函数时,若函数
为偶函数时,若函数![]() ,试证明:函数
,试证明:函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
解析:(1) 函数![]() 的定义域为R关于原点对称,………. 1分
的定义域为R关于原点对称,………. 1分
![]()
![]() 故此时函数
故此时函数![]() 是偶函数……….2分
是偶函数……….2分
![]()
![]()
![]() ,
,![]() 故函数
故函数![]() 不是奇函数,且易知此时
不是奇函数,且易知此时![]() 故函数
故函数![]() 也不是偶函数,所以
也不是偶函数,所以![]() 函数
函数![]() 是非奇非偶函数……….4分
是非奇非偶函数……….4分
(其他合理方式解答相应给分)
(2)![]()
![]() 为偶函数,由(1)知
为偶函数,由(1)知![]()
![]() ……….5分
……….5分
![]() ,则
,则![]() ……….7分
……….7分
=![]()
![]() ……………9分
……………9分
![]() ,则
,则![]() <0
<0
![]() ,
, ![]()
![]() 在
在![]() 上单调递减, ……….11分
上单调递减, ……….11分
![]() ,则
,则![]() >0
>0
![]() <0 ,
<0 , ![]()
![]() 在
在![]() 上单调递增, ……….13分
上单调递增, ……….13分

练习册系列答案
相关题目
 ,
,
 ∥
∥ 时,求
时,求 的值;
的值; 在
在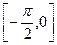 上的值域.
上的值域. 满足
满足 ,且
,且 是
是 ,
, 的等差中项.
的等差中项. ,
, ,求使
,求使
 成立的正整数
成立的正整数 的最小值.
的最小值. 过直线
过直线 和
和 的交点;
的交点;  垂直,求直线
垂直,求直线 到直线
到直线 的距离为1.求直线
的距离为1.求直线 ,过
,过 作直线
作直线 .
.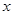 轴不垂直,交抛物线于A、B两点,是否存在
轴不垂直,交抛物线于A、B两点,是否存在 ,使得
,使得 ?若存在,求出m的值;若不存在,请说明理由?
?若存在,求出m的值;若不存在,请说明理由? 轴和
轴和 为定值,试证之;
为定值,试证之;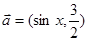 ,
,
 ∥
∥ 时,求
时,求 的值;
的值;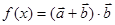 在
在 上的值域.
上的值域.