题目内容
已知函数f(x)=sin +cos
+cos ,g(x)=2sin2
,g(x)=2sin2 .
.
(1)若α是第一象限角,且f(α)= ,求g(α)的值;
,求g(α)的值;
(2)求使f(x)≥g(x)成立的x的取值集合.
 +cos
+cos ,g(x)=2sin2
,g(x)=2sin2 .
.(1)若α是第一象限角,且f(α)=
 ,求g(α)的值;
,求g(α)的值;(2)求使f(x)≥g(x)成立的x的取值集合.
(1) (2)
(2)
 (2)
(2)
f(x)=sin +cos
+cos =
= sinx-
sinx- cosx+
cosx+ cosx+
cosx+ sinx=
sinx= sinx,
sinx,
g(x)=2sin2 =1-cos x.
=1-cos x.
(1)由f(α)= 得sin α=
得sin α= .又α是第一象限角,所以cos α>0.
.又α是第一象限角,所以cos α>0.
从而g(α)=1-cos α=1- =1-
=1- =
= .
.
(2)f(x)≥g(x)等价于 sin x≥1-cos x,即
sin x≥1-cos x,即 sin x+cos x≥1,于是sin
sin x+cos x≥1,于是sin ≥
≥ ,
,
从而2kπ+ ≤x+
≤x+ ≤2kπ+
≤2kπ+ ,k∈Z,即2kπ≤x≤2kπ+
,k∈Z,即2kπ≤x≤2kπ+ ,k∈Z,
,k∈Z,
故使f(x)≥g(x)成立的x的取值集合为
 +cos
+cos =
= sinx-
sinx- cosx+
cosx+ cosx+
cosx+ sinx=
sinx= sinx,
sinx,g(x)=2sin2
 =1-cos x.
=1-cos x.(1)由f(α)=
 得sin α=
得sin α= .又α是第一象限角,所以cos α>0.
.又α是第一象限角,所以cos α>0.从而g(α)=1-cos α=1-
 =1-
=1- =
= .
.(2)f(x)≥g(x)等价于
 sin x≥1-cos x,即
sin x≥1-cos x,即 sin x+cos x≥1,于是sin
sin x+cos x≥1,于是sin ≥
≥ ,
,从而2kπ+
 ≤x+
≤x+ ≤2kπ+
≤2kπ+ ,k∈Z,即2kπ≤x≤2kπ+
,k∈Z,即2kπ≤x≤2kπ+ ,k∈Z,
,k∈Z,故使f(x)≥g(x)成立的x的取值集合为


练习册系列答案
相关题目
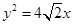 的焦点为椭圆
的焦点为椭圆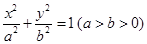 的右焦点,且椭圆的长轴长为4,M、N是椭圆上的的动点.
的右焦点,且椭圆的长轴长为4,M、N是椭圆上的的动点.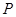 满足:
满足: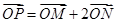 ,直线
,直线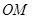 与
与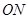 的斜率之积为
的斜率之积为 ,证明:存在定点
,证明:存在定点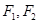 使
使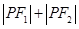 为定值,并求出
为定值,并求出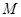 在第一象限,且点
在第一象限,且点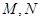 关于原点对称,
关于原点对称,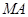 垂直于
垂直于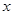 轴于点
轴于点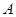 ,连接
,连接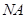 并延长交椭圆于点
并延长交椭圆于点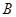 ,记直线
,记直线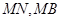 的斜率分别为
的斜率分别为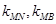 ,证明:
,证明: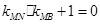 .
.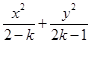 =1表示焦点在y轴上的椭圆,则实数k的取值范围是( )
=1表示焦点在y轴上的椭圆,则实数k的取值范围是( )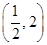
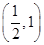
 +
+ =1(a>b>0)的左焦点F1作x轴的垂线交椭圆于点P,F2为右焦点,若∠F1PF2=60°,则椭圆的离心率为( )
=1(a>b>0)的左焦点F1作x轴的垂线交椭圆于点P,F2为右焦点,若∠F1PF2=60°,则椭圆的离心率为( )



 与椭圆
与椭圆 有相同的焦点,且双曲线
有相同的焦点,且双曲线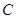 的渐近线方程为
的渐近线方程为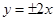 ,则双曲线
,则双曲线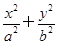 =1(a>b>0)的两个焦点分别为F1,F2,离心率为
=1(a>b>0)的两个焦点分别为F1,F2,离心率为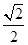 ,且过点(2,
,且过点(2,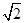 ).
).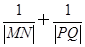 为定值.
为定值.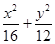 =1有共同的焦点F1,F2,且离心率互为倒数.若双曲线右支上一点P到右焦点F2的距离为4,则PF2的中点M到坐标原点O的距离等于________.
=1有共同的焦点F1,F2,且离心率互为倒数.若双曲线右支上一点P到右焦点F2的距离为4,则PF2的中点M到坐标原点O的距离等于________.