题目内容
有甲、乙两个班级进行数学考试,按照大于或等于85分为优秀,85分以下为非优秀统计成绩后,得到如下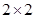 联表:
联表:
| | 优秀 | 非优秀 | 合计 |
| 甲班 | 30 | | |
| 乙班 | | 50 | |
| 合计 | | | 200 |
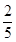
(1)请完成上面
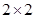 联表;
联表;(2)根据列联表的数据,能否有
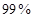 的把握认为“成绩与班级有关系”
的把握认为“成绩与班级有关系”(3)从全部200人中有放回抽取3次,每次抽取一人,记被抽取的3人中优秀的人数为
 ,若每次抽取得结果是相互独立的,求
,若每次抽取得结果是相互独立的,求 的分布列,期望
的分布列,期望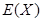 和方差
和方差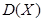
参考公式与参考数据如下:

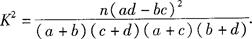
(1)
(2) 优秀 非优秀 合计 甲班 30 70 100 乙班 50 50 100 合计 80 120 200 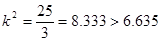 ,有
,有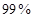 的把握
的把握
(3)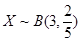 ,
,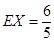 ,
,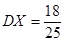
解析试题分析:(1)根据题意,由于全部200人中随机抽取1人为优秀的概率为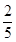 ,那么可知优秀的人数为80,那么可知不优秀的人数为120,那么可知得到列联表为:
,那么可知优秀的人数为80,那么可知不优秀的人数为120,那么可知得到列联表为:
(2)根据a=30,b=70,c=50,d=120,结合公式 优秀 非优秀 合计 甲班 30 70 100 乙班 50 50 100 合计 80 120 200 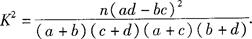 ,可知
,可知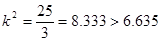 ,有
,有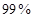 的把握认为“成绩与班级有关系”
的把握认为“成绩与班级有关系”
(3)由于全部200人中有放回抽取3次,每次抽取一人,记被抽取的3人中优秀的人数为 ,那么可知
,那么可知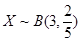 ,
,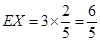 ,
,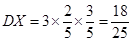 ,。
,。
考点:列联表和独立性检验
点评:主要是考查了独立性检验的思想的运用,以及二项分布的运用,属于中档题。

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案一台机器使用的时间较长,但还可以使用,它按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产有缺点零件的多少,随机器的运转的速度而变化,下表为抽样试验的结果:
| 转速x(转/秒) | 16 | 14 | 12 | 8 |
| 每小时生产有缺点的零件数y(件) | 11 | 9 | 8 | 5 |
画出散点图,并通过散点图确定变量y对x是否线性相关;
(2)如果y对x有线性相关关系,求回归直线方程;
(3)若实际生产中,允许每小时的产品中有缺点的零件最多为10个,那么机器的运转速度应控制在什么范围内?(精确到0.0001)
某中学号召本校学生在本学期参加市创办卫生城的相关活动,学校团委对该校学生是否关心创卫活动用简单抽样方法调查了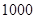 位学生(关心与不关心的各一半),
位学生(关心与不关心的各一半),
结果用二维等高条形图表示,如图.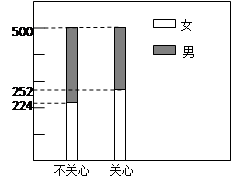
(1)完成列联表,并判断能否有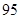 ℅的把握认为是否关心创卫活动与性别有关?
℅的把握认为是否关心创卫活动与性别有关?
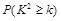 | 0.10 | 0.05 | 0.01 |
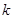 | 2.706 | 3.841 | 6.635 |
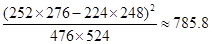
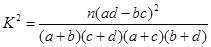 ;
;| | 女 | 男 | 合计 |
| 关心 | | | 500 |
| 不关心 | | | 500 |
| 合计 | | 524 | 1000 |
(2)已知校团委有青年志愿者100名,他们已参加活动的情况记录如下:
| 参加活动次数 | 1 | 2 | 3 |
| 人数 | 10 | 50 | 40 |
(i)从志愿者中任选两名学生,求他们参加活动次数恰好相等的概率;
(ii)从志愿者中任选两名学生,用
 表示这两人参加活动次数之差的绝对值,求随机变量
表示这两人参加活动次数之差的绝对值,求随机变量 的分布列及数学期望
的分布列及数学期望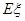 .
. 为调查某地区大学生是否爱好某项体育运动,用简单随机抽样方法从该地区的大学里调查了500位大学生,结果如下:
| | 男 | 女 |
| 爱好 | 40 | 30 |
| 不爱好 | 160 | 270 |
(2) 能否有99%的把握认为该地区的大学生是否爱好该项体育运动与性别有关?
附:
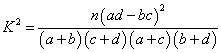
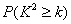 | 0.050 | 0.010 | 0.001 |
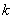 | 3.841 | 6.635 | 10.828 |
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(t)与相应的生产能耗y(t标准煤)的几组对照数据.
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程
 ;
;(3)已知该厂技术改造前100t甲产品的生产能耗为90t标准煤,试根据(2)求出的线性回归方程预测生产100t甲产品的生产能耗比技术改造前降低多少吨标准煤?
某校的研究性学习小组为了研究高中学生的身体发育状况,在该校随机抽出120名17至18周岁的男生,其中偏重的有60人,不偏重的也有60人。在偏重的60人中偏高的有40人,不偏高的有20人;在不偏重的60人中偏高和不偏高人数各占一半
(1)根据以上数据建立一个 列联表:
| | 偏重 | 不偏重 | 合计 |
| 偏高 | | | |
| 不偏高 | | | |
| 合计 | | | |
 ,第二类在
,第二类在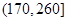 ,第三类在
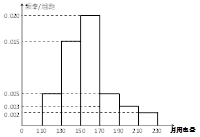
,第三类在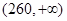 (单位:千瓦时). 某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图如图所示.
(单位:千瓦时). 某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图如图所示.