题目内容
某校的研究性学习小组为了研究高中学生的身体发育状况,在该校随机抽出120名17至18周岁的男生,其中偏重的有60人,不偏重的也有60人。在偏重的60人中偏高的有40人,不偏高的有20人;在不偏重的60人中偏高和不偏高人数各占一半
(1)根据以上数据建立一个 列联表:
| | 偏重 | 不偏重 | 合计 |
| 偏高 | | | |
| 不偏高 | | | |
| 合计 | | | |
(1) 列联表如下:
列联表如下:
(2)在犯错误的概率不超过0.10的前提下,认为该校17至18周岁的男生身高与体重有关 偏重 不偏重 合计 偏高 40 30 70 不偏高 20 30 50 合计 60 60 120
解析试题分析:(1) 列联表如下:
列联表如下:
6分 偏重 不偏重 合计 偏高 40 30 70 不偏高 20 30 50 合计 60 60 120
(2)根据列联表中的数据得到 的观测值为
的观测值为 , 10分
, 10分
而 ,因为
,因为 11分
11分
所以,在犯错误的概率不超过0.10的前提下,认为该校17至18周岁的男生身高与体重有关 12分
考点:本题考查了独立性检验的运用
点评:根据假设检验的思想,比较计算出的 与临界值的大小,选择接受假设还是拒绝假设.
与临界值的大小,选择接受假设还是拒绝假设.

 阅读快车系列答案
阅读快车系列答案在一段时间内,某种商品价格 (万元)和需求量
(万元)和需求量 之间的一组数据为:
之间的一组数据为:
价 格 | 1.4 | 1.6 | 1.8 | 2 | 2.2 |
需求量 | 12 | 10 | 7 | 5 | 3 |
(2)如果
 与
与 之间具有线性相关关系,求出回归直线方程,并预测当价格定为1.9万元,需求量大约是多少?(精确到0.01
之间具有线性相关关系,求出回归直线方程,并预测当价格定为1.9万元,需求量大约是多少?(精确到0.01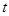 )
)参考公式及数据:
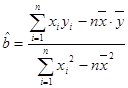 ,
,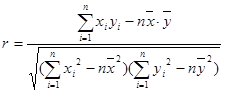 ,
,
相关性检验的临界值表:
| n-2 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 小概率0.01 | 1.000 | 0.990 | 0.959 | 0.917 | 0.874 | 0.834 | 0.798 | 0.765 | 0.735 | 0.708 |
有甲、乙两个班级进行数学考试,按照大于或等于85分为优秀,85分以下为非优秀统计成绩后,得到如下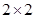 联表:
联表:
| | 优秀 | 非优秀 | 合计 |
| 甲班 | 30 | | |
| 乙班 | | 50 | |
| 合计 | | | 200 |
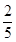
(1)请完成上面
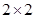 联表;
联表;(2)根据列联表的数据,能否有
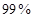 的把握认为“成绩与班级有关系”
的把握认为“成绩与班级有关系”(3)从全部200人中有放回抽取3次,每次抽取一人,记被抽取的3人中优秀的人数为
 ,若每次抽取得结果是相互独立的,求
,若每次抽取得结果是相互独立的,求 的分布列,期望
的分布列,期望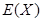 和方差
和方差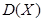
参考公式与参考数据如下:

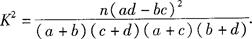
在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人。女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动。
(1)根据以上数据建立一个 的列联表;
的列联表;
(2)判断性别与休闲方式是否有关系。
(本题可以参考两个分类变量x和y有关系的可信度表:)
| P(k2>k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.83 |
某校为了解高二学生 、
、 两个学科学习成绩的合格情况是否有关, 随机抽取了该年级一次期末考试
两个学科学习成绩的合格情况是否有关, 随机抽取了该年级一次期末考试 、
、 两个学科的合格人数与不合格人数,得到以下2
两个学科的合格人数与不合格人数,得到以下2 2列联表:
2列联表:
| |  学科合格人数 学科合格人数 |  学科不合格人数 学科不合格人数 | 合计 |
 学科合格人数 学科合格人数 | 40 | 20 | 60 |
 学科不合格人数 学科不合格人数 | 20 | 30 | 50 |
| 合计 | 60 | 50 | 110 |
 学科合格”与“
学科合格”与“ 学科合格”有关;
学科合格”有关;(2)从“
 学科合格”的学生中任意抽取2人,记被抽取的2名学生中“
学科合格”的学生中任意抽取2人,记被抽取的2名学生中“ 学科合格”的人数为
学科合格”的人数为 ,求
,求 的数学期望.
的数学期望.附公式与表:

 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛. 为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计. 请你根据尚未完成并有局部污损的频率分布表和频数分布直方图,解答下列问题:
(1)填充频率分布表的空格(将答案直接填在表格内);
| 分组 | 频数 | 频率 |
| 50.5~60.5 | 4 | 0.08 |
| 60.5~70.5 | | 0.16 |
| 70.5~80.5 | 10 | |
| 80.5~90.5 | 16 | 0.32 |
| 90.5~100.5 | | |
| 合计 | 50 | |
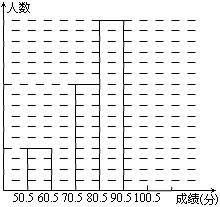
(3)若成绩在75.5~85.5分的学生为二等奖,问获得二等奖的学生约为多少人。
 (单位:t,100≤
(单位:t,100≤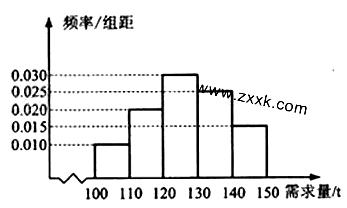

 内.现根据所得数据画出了该样本的频率分布直方图如下.(每个分组包括左端点,不包括右端点,如第一组表示月收入在
内.现根据所得数据画出了该样本的频率分布直方图如下.(每个分组包括左端点,不包括右端点,如第一组表示月收入在 内)
内)
 内的频率;
内的频率; 内的居民中抽取多少人?
内的居民中抽取多少人?