题目内容
设函数,则f(x)=sin(2x+
)+cos(2x+
),则( )
| π |
| 4 |
| π |
| 4 |
A.y=f(x)在(0,
| ||||
B.y=f(x)在(0,
| ||||
C.y=f(x)在(0,
| ||||
D.y=f(x)在(0,
|
因为f(x)=sin(2x+
)+cos(2x+
)=
sin(2x+
)=
cos2x.
它的对称轴方程可以是:x=
;所以A,C错误;函数y=f(x)在(0,
)单调递减,所以B错误;D正确.
故选D
| π |
| 4 |
| π |
| 4 |
| 2 |
| π |
| 2 |
| 2 |
它的对称轴方程可以是:x=
| π |
| 2 |
| π |
| 2 |
故选D

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设函数,则f(x)=sin(2x+
)+cos(2x+
),则( )
| π |
| 4 |
| π |
| 4 |
A、y=f(x)在(0,
| ||||
B、y=f(x)在(0,
| ||||
C、y=f(x)在(0,
| ||||
D、y=f(x)在(0,
|
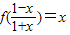 ,则f(x)的表达式( )
,则f(x)的表达式( )
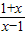


 ,则f(x)=0( )
,则f(x)=0( ) ,则f(x)的表达式( )
,则f(x)的表达式( )


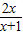
 ,则f(x)的表达式( )
,则f(x)的表达式( )


