题目内容
设函数 ,则f(x)=0( )
,则f(x)=0( )A.在定义域内无解
B.存在两个解,且分别在(-∞,2011)、(2012,+∞)内
C.存在两个解,且分别在(-∞,-2010)、(2010,+∞)内
D.存在两个解,都在(2011,2012)内
【答案】分析:由已知中函数f(x)的解析式,可得f(2011)>0,f(2012)>0,f(2011 )<0,进而根据函数零点存在定理可得,函数f(x)在区间(2011,2011
)<0,进而根据函数零点存在定理可得,函数f(x)在区间(2011,2011 )和区间(2011
)和区间(2011 ,2012)上各有一个零点,即函数f(x)在区间(2011,2012)上有两个零点,即方程f(x)=0在区间(2011,2012)上有两个实根.
,2012)上各有一个零点,即函数f(x)在区间(2011,2012)上有两个零点,即方程f(x)=0在区间(2011,2012)上有两个实根.
解答:解:∵ ,
,
∴f(2011)= >0
>0
f(2012)= >0
>0
又∵f(2011 )=
)= •(-
•(- )+
)+ =
= -
- <0
<0
故函数f(x)在区间(2011,2011 )和区间(2011
)和区间(2011 ,2012)上各有一个零点
,2012)上各有一个零点
故f(x)=0存在两个解,都在(2011,2012)内
故选D
点评:本题考查的知识点是根的存在性及根的个数判断,熟练掌握函数的零点与对应方程根之间的关系是解答的关键.
 )<0,进而根据函数零点存在定理可得,函数f(x)在区间(2011,2011
)<0,进而根据函数零点存在定理可得,函数f(x)在区间(2011,2011 )和区间(2011
)和区间(2011 ,2012)上各有一个零点,即函数f(x)在区间(2011,2012)上有两个零点,即方程f(x)=0在区间(2011,2012)上有两个实根.
,2012)上各有一个零点,即函数f(x)在区间(2011,2012)上有两个零点,即方程f(x)=0在区间(2011,2012)上有两个实根.解答:解:∵
 ,
,∴f(2011)=
 >0
>0f(2012)=
 >0
>0又∵f(2011
 )=
)= •(-
•(- )+
)+ =
= -
- <0
<0故函数f(x)在区间(2011,2011
 )和区间(2011
)和区间(2011 ,2012)上各有一个零点
,2012)上各有一个零点故f(x)=0存在两个解,都在(2011,2012)内
故选D
点评:本题考查的知识点是根的存在性及根的个数判断,熟练掌握函数的零点与对应方程根之间的关系是解答的关键.

练习册系列答案
 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
设函数,则f(x)=sin(2x+
)+cos(2x+
),则( )
| π |
| 4 |
| π |
| 4 |
A、y=f(x)在(0,
| ||||
B、y=f(x)在(0,
| ||||
C、y=f(x)在(0,
| ||||
D、y=f(x)在(0,
|
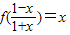 ,则f(x)的表达式( )
,则f(x)的表达式( )
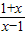


 ,则f(x)的表达式( )
,则f(x)的表达式( )


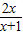
 ,则f(x)的表达式( )
,则f(x)的表达式( )


