题目内容
17.已知△ABC是锐角三角形,角A,B,C所对的边分别是a,b,c,(1)若a,b,c成等比数列,求角B的最大值,并判断此时△ABC的形状;
(2)若A,B,C成等差数列,求sinA+sinC的取值范围.
分析 (1)由等比数列性质可求b2=ac,利用余弦定理可得cosB$≥\frac{1}{2}$,利用余弦函数的图象和性质即可解得B的最大值是$\frac{π}{3}$,当且仅当a=c时取“=”,即可判定此时三角ABC是等边三角形.
(2)由等差数列性质可得,2B=A+C,解得B=60°,化简sinA+sinC可得$\sqrt{3}$sin(30°+C),结合范围$\left\{{\begin{array}{l}{{0°}<C<{{90}°}}\\{{0°}<{{120}°}-C<{{90}°}}\end{array}}\right.$,利用正弦函数的图象和性质即可求得其范围.
解答 解:(1)∵a,b,c成等比数列,
∴b2=ac,
∴$cosB=\frac{{{a^2}+{c^2}-{b^2}}}{2ac}=\frac{{{a^2}+{c^2}-ac}}{2ac}≥\frac{2ac-ac}{2ac}=\frac{1}{2}$.…(3分)
当且仅当a=c时取“=”,
∴B的最大值是$\frac{π}{3}$,此时三角ABC是等边三角形.…(5分)
(2)∵A,B,C成等差数列,
∴2B=A+C,
∴B=60°…(6分)
∴$sinA+sinC=sin({120°}-C)+sinC=\frac{{\sqrt{3}}}{2}cosC+\frac{3}{2}sinC=\sqrt{3}sin({30°}+C)$,…(7分)
∵$\left\{{\begin{array}{l}{{0°}<C<{{90}°}}\\{{0°}<{{120}°}-C<{{90}°}}\end{array}}\right.$,
∴30°<C<90°,
∴60°<30°+C<120°,
∴$\frac{3}{2}<\sqrt{3}sin({30°}+C)≤\sqrt{3}$.
∴$\frac{3}{2}<sinA+sinC≤\sqrt{3}$.…(10分)
点评 本题主要考查了等比数列、等差数列的性质的应用,考查了余弦定理,余弦函数的图象和性质,正弦函数的图象和性质的应用,属于中档题.

| A. | x+y-2=0 | B. | x-y+2=0 | C. | x+y-3=0 | D. | x-y+3=0 |
| A. | {1} | B. | [0,1] | C. | (0,1] | D. | [0,1) |
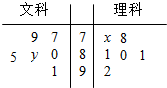 某中学从文、理科实验班中各选6名同学去参加复旦大学自主招生考试,其数学成绩茎叶图如图,其中文科生的成绩的众数为85,理科生成绩平均数为81,则x•y的值为( )
某中学从文、理科实验班中各选6名同学去参加复旦大学自主招生考试,其数学成绩茎叶图如图,其中文科生的成绩的众数为85,理科生成绩平均数为81,则x•y的值为( )