题目内容
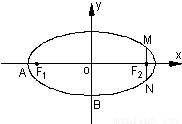
设椭圆C: 的左、右焦点分别为F1、F2,上顶点为A,在x轴负半轴上有一点B,满足
的左、右焦点分别为F1、F2,上顶点为A,在x轴负半轴上有一点B,满足 ,且AB⊥AF2.
,且AB⊥AF2.(Ⅰ)求椭圆C的离心率;
(Ⅱ)若过A、B、F2三点的圆恰好与直线
 相切,求椭圆C的方程;
相切,求椭圆C的方程; (Ⅲ)在(Ⅱ)的条件下,过右焦点F2作斜率为k的直线l与椭圆C交于M、N两点,若点P(m,0)使得以PM,PN为邻边的平行四边形是菱形,求的取值范围.

【答案】分析:(Ⅰ)由题意知F1(-c,0),F2(c,0),A(0,b),由 知F1为BF2的中点,由AB⊥AF2,知Rt△ABF2中,BF22=AB2+AF22
知F1为BF2的中点,由AB⊥AF2,知Rt△ABF2中,BF22=AB2+AF22 ,由此能求出椭圆的离心率.
,由此能求出椭圆的离心率.
(Ⅱ)由 ,知
,知 ,
, ,
, ,Rt△ABF2的外接圆圆心为(-
,Rt△ABF2的外接圆圆心为(- ,0),半径r=a,所以
,0),半径r=a,所以 ,由此能求出椭圆方程.
,由此能求出椭圆方程.
(Ⅲ)由F2(1,0),l:y=k(x-1),设M(x1,y1),N(x2,y2),由 ,得(3+4k2)x2-8k2x+4k2-12=0,由此能求出m的取值范围.
,得(3+4k2)x2-8k2x+4k2-12=0,由此能求出m的取值范围.
解答:解:(Ⅰ)由题意知F1(-c,0),F2(c,0),A(0,b)
∵ 知F1为BF2的中点,
知F1为BF2的中点,
AB⊥AF2
∴Rt△ABF2中,BF22=AB2+AF22 ,
,
又a2=b2+c2
∴a=2c
故椭圆的离心率 …(3分)
…(3分)
(Ⅱ)由(Ⅰ)知 得
得 ,
,
于是 ,
, ,
,
Rt△ABF2的外接圆圆心为(- ,0),半径r=a,
,0),半径r=a,
所以 ,解得a=2,
,解得a=2,
∴c=1, ,
,
所求椭圆方程为 …(6分)
…(6分)
(Ⅲ)由(Ⅱ)知F2(1,0),l:y=k(x-1),
设M(x1,y1),N(x2,y2),
由 ,代入得(3+4k2)x2-8k2x+4k2-12=0
,代入得(3+4k2)x2-8k2x+4k2-12=0
则 ,
,
y1+y2=k(x1+x2-2)…(8分)

由于菱形对角线垂直,
则
故x1+x2-2m+k(y1+y2)=0
即x1+x2-2m+k2(x1+x2-2)=0,
 …(10分)
…(10分)
由已知条件知k≠0,
∴
∴ 故m的取值范围是
故m的取值范围是 .…(12分)
.…(12分)
点评:本题主要考查椭圆标准方程,简单几何性质,直线与椭圆的位置关系,圆的简单性质等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.
 知F1为BF2的中点,由AB⊥AF2,知Rt△ABF2中,BF22=AB2+AF22
知F1为BF2的中点,由AB⊥AF2,知Rt△ABF2中,BF22=AB2+AF22 ,由此能求出椭圆的离心率.
,由此能求出椭圆的离心率.(Ⅱ)由
 ,知
,知 ,
, ,
, ,Rt△ABF2的外接圆圆心为(-
,Rt△ABF2的外接圆圆心为(- ,0),半径r=a,所以
,0),半径r=a,所以 ,由此能求出椭圆方程.
,由此能求出椭圆方程.(Ⅲ)由F2(1,0),l:y=k(x-1),设M(x1,y1),N(x2,y2),由
 ,得(3+4k2)x2-8k2x+4k2-12=0,由此能求出m的取值范围.
,得(3+4k2)x2-8k2x+4k2-12=0,由此能求出m的取值范围.解答:解:(Ⅰ)由题意知F1(-c,0),F2(c,0),A(0,b)
∵
 知F1为BF2的中点,
知F1为BF2的中点,AB⊥AF2
∴Rt△ABF2中,BF22=AB2+AF22
 ,
,又a2=b2+c2
∴a=2c
故椭圆的离心率
 …(3分)
…(3分)(Ⅱ)由(Ⅰ)知
 得
得 ,
,于是
 ,
, ,
,Rt△ABF2的外接圆圆心为(-
 ,0),半径r=a,
,0),半径r=a,所以
 ,解得a=2,
,解得a=2,∴c=1,
 ,
,所求椭圆方程为
 …(6分)
…(6分)(Ⅲ)由(Ⅱ)知F2(1,0),l:y=k(x-1),
设M(x1,y1),N(x2,y2),
由
 ,代入得(3+4k2)x2-8k2x+4k2-12=0
,代入得(3+4k2)x2-8k2x+4k2-12=0则
 ,
,y1+y2=k(x1+x2-2)…(8分)

由于菱形对角线垂直,
则

故x1+x2-2m+k(y1+y2)=0
即x1+x2-2m+k2(x1+x2-2)=0,
 …(10分)
…(10分)由已知条件知k≠0,
∴

∴
 故m的取值范围是
故m的取值范围是 .…(12分)
.…(12分)点评:本题主要考查椭圆标准方程,简单几何性质,直线与椭圆的位置关系,圆的简单性质等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.

练习册系列答案
相关题目
 如图,在直角坐标系xOy中,已知椭圆C:
如图,在直角坐标系xOy中,已知椭圆C:
 =1(a>b>0)的左、右两个焦 点。(1)若椭圆C上的点A(1,
=1(a>b>0)的左、右两个焦 点。(1)若椭圆C上的点A(1, )到F1、F2两点的 距离之和等于4,写出椭圆C的方程和焦点坐标;
)到F1、F2两点的 距离之和等于4,写出椭圆C的方程和焦点坐标; +
+ =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的
,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的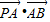 =m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.
=m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.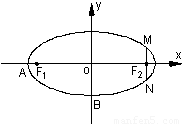
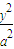 +
+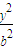 =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e=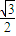 ,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的
,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的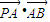 =m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.
=m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.