题目内容
设锐角△ABC的三内角A,B,C的对边分别为 a,b,c,向量| m |
| 3 |
| n |
| 3 |
| 2 |
| m |
| n |
(Ⅰ)求角A的大小;
(Ⅱ)若a=2,c=4
| 3 |
| 3 |
分析:(Ⅰ)利用向量平行,得到关于A的关系式,利用二倍角公式、两角差的正弦函数化简,求出角A的大小;
(Ⅱ)通过a=2,c=4
sinB,且△ABC的面积小于
,得到B的余弦值的范围,然后求角B的取值范围.
(Ⅱ)通过a=2,c=4
| 3 |
| 3 |
解答:解:(Ⅰ)因为
∥
,则sinA(sinA+
cosA)=
,即sin2A+
sinAcosA=
、(2分)
所以
+
sin2A=
,即
sin2A-
cos2A=1,即sin(2A-
)=1、(5分)
A是锐角,则2A-
=
,
所以A=
、(6分)
(Ⅱ)因为a=2,c=4
sinB,
则S△ABC=
acsinB=
×2×4
sin2B=4
sin2B=4
×
=2
-2
cos2B、(9分)
由已知,2
-2
cos2B<
,即cos2B>
、(11分)
因为B是锐角,
所以0<2B<
,即0<B<
,故角B的取值范围是(0,
)、(13分)
| m |
| n |
| 3 |
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
所以
| 1-cos2A |
| 2 |
| ||
| 2 |
| 3 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
A是锐角,则2A-
| π |
| 6 |
| π |
| 2 |
所以A=
| π |
| 3 |
(Ⅱ)因为a=2,c=4
| 3 |
则S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| 1-cos2B |
| 2 |
| 3 |
| 3 |
由已知,2
| 3 |
| 3 |
| 3 |
| 1 |
| 2 |
因为B是锐角,
所以0<2B<
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
点评:本题是中档题,考查向量的平行关系的应用,三角函数的二倍角公式、两角差正弦函数的应用,考查解三角形的面积等知识,考查计算能力.

练习册系列答案
相关题目
 且
且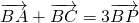 则下列正确的命题序号是________.
则下列正确的命题序号是________. 且
且 则下列正确的命题序号是 .
则下列正确的命题序号是 .