题目内容
下列函数中,既在(0,π)上是增函数,又是以2π为最小正周期的偶函数是
- A.y=|sinx|
- B.y=1-
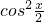
- C.y=2cosx
- D.y=tan

B
分析:题目中有“在(0,π)上单调递增,以2π为最小正周期,偶函数”三个条件,只要有一个不满足,就可以排除.
由于|sin(x+π)|=|sinx|?y=|sinx|是以π为最小正周期的函数,可排除A;y=2cosx在(0,π)上是减函数,可排除C;
y=tan 为奇函数,可排除D;问题即可解决.
为奇函数,可排除D;问题即可解决.
解答:∵|sin(x+π)|=|sinx|,
∴y=|sinx|是以π为最小正周期的函数,可排除A;
又y=2cosx在(0,π)上是减函数,可排除C;
∵tan(- )=-tan
)=-tan ,
,
∴y=tan 为奇函数,可排除D;
为奇函数,可排除D;
y=1-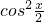 =
= -
- cosx满足“在(0,π)上单调递增,以2π为最小正周期,偶函数”三个条件,因此B正确.
cosx满足“在(0,π)上单调递增,以2π为最小正周期,偶函数”三个条件,因此B正确.
故选B.
点评:本题考查余弦函数的单调性及奇偶性,二倍角的余弦及三角函数的周期性,着重考查三角函数的性质及应用,属于中档题.
分析:题目中有“在(0,π)上单调递增,以2π为最小正周期,偶函数”三个条件,只要有一个不满足,就可以排除.
由于|sin(x+π)|=|sinx|?y=|sinx|是以π为最小正周期的函数,可排除A;y=2cosx在(0,π)上是减函数,可排除C;
y=tan
 为奇函数,可排除D;问题即可解决.
为奇函数,可排除D;问题即可解决.解答:∵|sin(x+π)|=|sinx|,
∴y=|sinx|是以π为最小正周期的函数,可排除A;
又y=2cosx在(0,π)上是减函数,可排除C;
∵tan(-
 )=-tan
)=-tan ,
,∴y=tan
 为奇函数,可排除D;
为奇函数,可排除D;y=1-
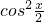 =
= -
- cosx满足“在(0,π)上单调递增,以2π为最小正周期,偶函数”三个条件,因此B正确.
cosx满足“在(0,π)上单调递增,以2π为最小正周期,偶函数”三个条件,因此B正确.故选B.
点评:本题考查余弦函数的单调性及奇偶性,二倍角的余弦及三角函数的周期性,着重考查三角函数的性质及应用,属于中档题.

练习册系列答案
相关题目
下列函数中,既为偶函数又在(0,π)上单调递增的是( )
| A、y=tan|x| | ||
| B、y=cos(-x) | ||
C、y=sin(x-
| ||
D、y=|cot
|

