题目内容
已知数列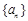 为等比数列,其前n项和为
为等比数列,其前n项和为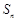 ,且满足
,且满足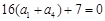 ,
,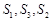 成等差数列.
成等差数列.
(1)求数列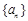 的通项公式;
的通项公式;
(2)已知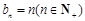 ,记
,记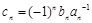 ,求数列
,求数列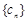 前n项和
前n项和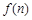 .
.
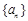 为等比数列,其前n项和为
为等比数列,其前n项和为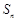 ,且满足
,且满足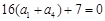 ,
,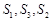 成等差数列.
成等差数列.(1)求数列
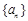 的通项公式;
的通项公式;(2)已知
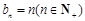 ,记
,记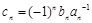 ,求数列
,求数列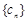 前n项和
前n项和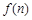 .
.(1) ;(2)
;(2)  .
.
 ;(2)
;(2)  .
.试题分析:(1)利用
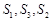 成等差数列,所以
成等差数列,所以 ,将其转化为关于
,将其转化为关于 的方程,再代入
的方程,再代入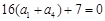 求其首项,从而得到等比数列的通项公式;
求其首项,从而得到等比数列的通项公式;(2)将
 化简得到
化简得到 ,这属于等差数列
,这属于等差数列 等比数列的形式,和
等比数列的形式,和 用错位相减法求其和,先列出
用错位相减法求其和,先列出 ,再列出2
,再列出2 ,两式相减,化简得到结果.
,两式相减,化简得到结果.试题解析:(1)设
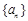 的公比为q, ∵
的公比为q, ∵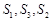 成等差数列,
成等差数列,∴
 1分
1分∴
 , 化简得
, 化简得 ,
,∴
 3分
3分又
 ,∴
,∴ ,
, 6分
6分(2)∵
 ,
, ,∴
,∴ 8分
8分∴
 ,
,2
 ,
,∴
 , 11分
, 11分∴
 12分
12分
练习册系列答案
相关题目
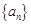 满足:
满足: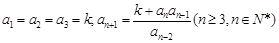 其中
其中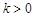 ,数列
,数列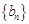 满足:
满足: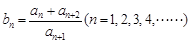
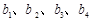 ;
; 是各项为不同的正数的等差数列,
是各项为不同的正数的等差数列, 成等差数列,又
成等差数列,又 .
. 为等比数列;
为等比数列; ,求数列
,求数列 为数列
为数列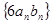 的前
的前 项和,求
项和,求 .
. 为正项等比数列,
为正项等比数列, ,
, ,
, 为等差数列
为等差数列 的前
的前
 ,
, .
. ,求
,求 .
.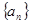 为等差数列,且
为等差数列,且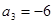 ,
,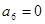 .
.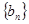 满足
满足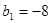 ,
,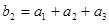 ,求数列
,求数列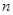 项和公式.
项和公式.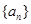 中,
中,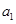 =1,
=1,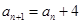 ,则
,则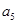 的值为____________.
的值为____________. 满足:对于
满足:对于 都有
都有 ,若
,若 ,则
,则 的通项公式为( )
的通项公式为( )


