题目内容
已知 =(cos
=(cos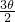 ,sin
,sin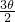 ),
), =(cos
=(cos ,-sin
,-sin ),且θ∈[0,
),且θ∈[0, ].
].
(1)若| +
+ |=1,试求θ的值;
|=1,试求θ的值;
(2)求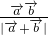 的最值.
的最值.
解:(1)由题意可得  •
• =cos
=cos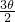 cos
cos +sin
+sin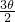 (-sin
(-sin )=cos(
)=cos(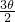 +
+ )=cos2θ,
)=cos2θ,
∴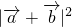 =
= +
+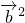 +
+ •
• =2+2cos2θ=4cos2θ=1,∴cosθ=
=2+2cos2θ=4cos2θ=1,∴cosθ= .
.
再由θ∈[0, ]可得 θ=
]可得 θ= .
.
(2)∵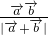 =
=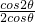 =cosθ-
=cosθ-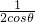 ,令 t=cosθ,则有
,令 t=cosθ,则有 ≤t≤1,∴(t-
≤t≤1,∴(t-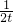 )′=1+
)′=1+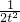 >0,
>0,
∴(t-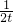 ) 在[
) 在[ ,1]上是增函数,故当t=
,1]上是增函数,故当t= 时,(t-
时,(t-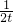 ) 取得最小值为-
) 取得最小值为- ,当t=1时,(t-
,当t=1时,(t-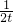 ) 取得最大值为
) 取得最大值为  .
.
分析:(1)利用两个向量的数量积公式求出 •
• 的值,再由
的值,再由 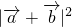 =1求出cosθ=
=1求出cosθ= ,再由θ的范围求出θ的值.
,再由θ的范围求出θ的值.
(2)化简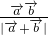 为cosθ-
为cosθ-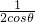 ,令 t=cosθ,则有
,令 t=cosθ,则有 ≤t≤1,利用导数判断函数 (t-
≤t≤1,利用导数判断函数 (t-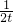 ) 在[
) 在[ ,1]上是增函数,由此求得函数的最值.
,1]上是增函数,由此求得函数的最值.
点评:本题主要考查两个向量的数量积公式的应用,根据三角函数的值求角,利用导数研究函数的单调性,求函数的最值,属于中档题.
 •
• =cos
=cos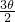 cos
cos +sin
+sin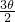 (-sin
(-sin )=cos(
)=cos(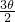 +
+ )=cos2θ,
)=cos2θ,∴
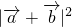 =
= +
+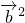 +
+ •
• =2+2cos2θ=4cos2θ=1,∴cosθ=
=2+2cos2θ=4cos2θ=1,∴cosθ= .
.再由θ∈[0,
 ]可得 θ=
]可得 θ= .
.(2)∵
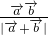 =
=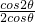 =cosθ-
=cosθ-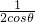 ,令 t=cosθ,则有
,令 t=cosθ,则有 ≤t≤1,∴(t-
≤t≤1,∴(t-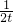 )′=1+
)′=1+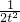 >0,
>0,∴(t-
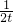 ) 在[
) 在[ ,1]上是增函数,故当t=
,1]上是增函数,故当t= 时,(t-
时,(t-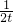 ) 取得最小值为-
) 取得最小值为- ,当t=1时,(t-
,当t=1时,(t-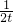 ) 取得最大值为
) 取得最大值为  .
.分析:(1)利用两个向量的数量积公式求出
 •
• 的值,再由
的值,再由 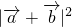 =1求出cosθ=
=1求出cosθ= ,再由θ的范围求出θ的值.
,再由θ的范围求出θ的值.(2)化简
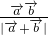 为cosθ-
为cosθ-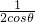 ,令 t=cosθ,则有
,令 t=cosθ,则有 ≤t≤1,利用导数判断函数 (t-
≤t≤1,利用导数判断函数 (t-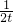 ) 在[
) 在[ ,1]上是增函数,由此求得函数的最值.
,1]上是增函数,由此求得函数的最值.点评:本题主要考查两个向量的数量积公式的应用,根据三角函数的值求角,利用导数研究函数的单调性,求函数的最值,属于中档题.

练习册系列答案
相关题目