题目内容
设函数![]() .
.
(1)求函数![]() 的单调递增区间;
的单调递增区间;
(2)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 内恰有两个相异的实根,求实数
内恰有两个相异的实根,求实数![]() 的取值范围.
的取值范围.
解析:(1)函数![]() 的定义域为
的定义域为![]() ,
,
∵![]() ,
,
∵![]() ,则使
,则使![]() 的
的![]() 的取值范围为
的取值范围为![]() ,
,
故函数![]() 的单调递增区间为
的单调递增区间为![]() .
.
(2)方法1:∵![]() ,
,
∴![]() .
.
令![]() ,
,
∵![]() ,且
,且![]() ,
,
由![]() .
.
∴![]() 在区间
在区间![]() 内单调递减,在区间
内单调递减,在区间![]() 内单调递增,
内单调递增,
故![]() 在区间
在区间![]() 内恰有两个相异实根
内恰有两个相异实根
即 解得:
解得:![]() .
.
综上所述,![]() 的取值范围是
的取值范围是![]() .
.
方法2:∵![]() ,
,
∴![]() .
.
即![]() ,
,
令![]() ,
,
∵![]() ,且
,且![]() ,
,
由![]() .
.
∴![]() 在区间
在区间![]() 内单调递增,在区间
内单调递增,在区间![]() 内单调递减.
内单调递减.
∵![]() ,
,![]() ,
,![]() ,
,
又![]() ,
,
故![]() 在区间
在区间![]() 内恰有两个相异实根
内恰有两个相异实根![]() .
.
即![]() .
.

练习册系列答案
相关题目
 设函数
设函数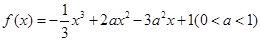 ,
,
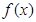 的极大值;
的极大值; ,若
,若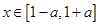 时,恒有
时,恒有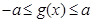 成立,试确定实数
成立,试确定实数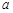 的取值范围.
的取值范围.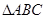 中,角
中,角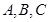 的对边分别为
的对边分别为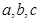 ,且
,且
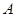 ;
;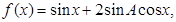 将函数
将函数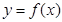 的图象上各点的纵坐标保持不变,横坐标缩短到原来的
的图象上各点的纵坐标保持不变,横坐标缩短到原来的 ,把所得图象向右平移
,把所得图象向右平移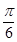 个单位,得到函数
个单位,得到函数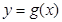 的图象,求函数
的图象,求函数