题目内容
奇函数 在区间
在区间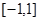 上是增函数,且
上是增函数,且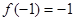 ,当
,当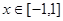 时,函数
时,函数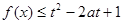 对一切
对一切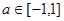 恒成立,则实数
恒成立,则实数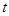 的取值范围是 ( )
的取值范围是 ( )
A. | B.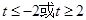 |
C.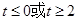 | D.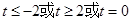 |
D
解析试题分析:奇函数f(x)在[-1,1]上是增函数,且f(-1)=-1,在[-1,1]最大值是1,∴1≤t2-2at+1,当t=0时显然成立,当t≠0时,则t2-2at≥0成立,又a∈[-1,1],令g(a)=2at-t2,a∈[-1,1],当t>0时,g(a)是减函数,故令g(1)≥0,解得t≥2,当t<0时,g(a)是增函数,故令g(-1)≥0,解得t≤-2,综上知,t≥2或t≤-2或t=0.选D.
考点:1.函数的单调性;2.函数的奇偶性;3.函数恒成立问题的应用

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
设函数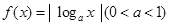 的定义域为
的定义域为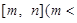
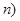 ,值域为
,值域为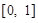 ,若
,若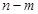 的最小值为
的最小值为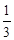 ,则实数a的值为( )
,则实数a的值为( )
A.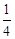 | B.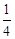 或 或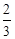 | C.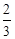 | D.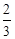 或 或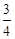 |
函数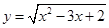 的定义域是( )
的定义域是( )
A.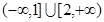 | B. | C.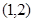 | D. |
已知 是函数f(x)=lnx-(
是函数f(x)=lnx-(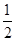 )x的零点,若
)x的零点,若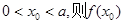 的值满足( )
的值满足( )
A.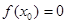 | B.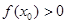 |
C.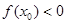 | D.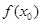 的符号不确定 的符号不确定 |
函数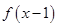 是
是 上的奇函数,
上的奇函数,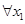 、
、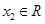 ,
,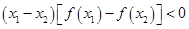 ,则
,则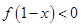 的解集是( )
的解集是( )
A.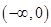 | B.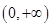 | C. | D.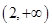 |
函数 在
在 上为减函数,则
上为减函数,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
设奇函数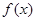 满足
满足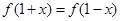 ,当
,当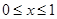 时,
时,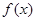 =
=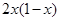 ,则
,则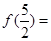 ( )
( )
A.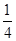 | B.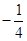 | C.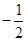 | D.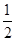 |
偶函数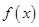 在
在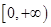 上为减函数,不等式
上为减函数,不等式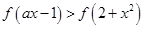 恒成立,则
恒成立,则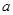 的取值范围是( )
的取值范围是( )
A.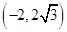 | B.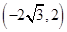 | C.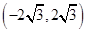 | D.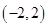 |
函数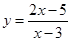 的值域是
的值域是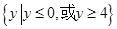 ,则此函数的定义域为( )
,则此函数的定义域为( )
A.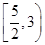 | B.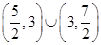 | C.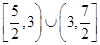 | D.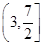 |