题目内容
抛物线的焦点为椭圆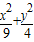
=1的左焦点，顶点在椭圆中心，则抛物线方程为 ．
【答案】分析：先求出椭圆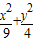
=1的左焦点即位抛物线的焦点，再利用焦点的横坐标与系数2p的关系求出p；即可求出抛物线方程．
解答：解：因为椭圆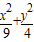
=1的左焦点为（-
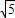.0），所以
=
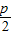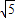，2p=4
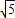且抛物线开口向左．
所以抛物线方程为y2=-4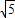
x．
故答案为：y2=-4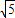
x．
点评：本题考查抛物线标准方程的求法．在求抛物线的标准方程时，一定要先判断出开口方向，再设方程．
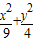=1的左焦点即位抛物线的焦点，再利用焦点的横坐标与系数2p的关系求出p；即可求出抛物线方程．解答：解：因为椭圆
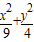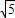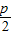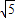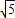=1的左焦点为（-.0），所以=，2p=4且抛物线开口向左．所以抛物线方程为y2=-4
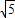x．故答案为：y2=-4
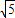x．点评：本题考查抛物线标准方程的求法．在求抛物线的标准方程时，一定要先判断出开口方向，再设方程．
练习册系列答案
阅读快车系列答案
相关题目
的右焦点F，且交椭圆C于A，B两点，点A，F，B在直线
上的射影依次为点D，K，E.
的焦点为椭圆C的上顶点，求椭圆C的方程；
，当m变化时，求
的值；
的右焦点F，且交椭圆C于A，B两点，点A，F，B在直线
上的射影依次为点D，K，E.
的焦点为椭圆C的上顶点，求椭圆C的方程；
的左焦点，顶点在椭圆中心，则抛物线方程为