Question

（08年大连24中） （12分）    如图，已知直线的右焦点F，且交椭圆C于A，B两点，点A，F，B在直线上的射影依次为点D，K，E.

   （1）若抛物线的焦点为椭圆C的上顶点，求椭圆C的方程；

   （2）对于（1）中的椭圆C，若直线L交y轴于点M，且，当m变化时，求的值；

   （3）连接AE，BD，试探索当m变化时，直线AE、BD是否相交于一定点N？若交于定点N，请求出N点的坐标，并给予证明；否则说明理由.

 

Answer 1

解析:（1）易知

      

       …………………………………………2分

   （2）

       设

      

       …………………………………………4分

       又由

      

       同理

      

       ……………………………………6分

   （3）

       先探索，当m=0时，直线L⊥ox轴，则ABED为矩形，由对称性知，AE与BD相交FK中点N，且

       猜想：当m变化时，AE与BD相交于定点……………………8分

       证明：设

       当m变化时首先AE过定点N

      

      

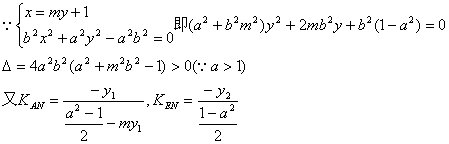
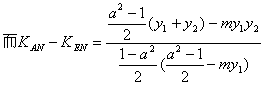
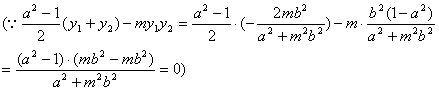
       A、N、E三点共线

       同理可得B、N、D三点共线

       ∴AE与BD相交于定点……………………12分