题目内容
非空集合 关于运算
关于运算 满足:
满足:
(1)对任意 ,都有
,都有 ;
;
(2)存在 ,使得对一切
,使得对一切 ,都有
,都有 ,则称
,则称 关于运算
关于运算 为“融洽集”;现给出下列集合和运算:
为“融洽集”;现给出下列集合和运算:

 ① ②
① ②
③

 ④
④
 ⑤
⑤
其中 关于运算
关于运算 为“融洽集”____________。(写出所有“融洽集”的序号)
为“融洽集”____________。(写出所有“融洽集”的序号)
【答案】
①③
【解析】解:根据题意我们可知(1)当a,b都为非负整数时,a,b通过加法运算还是非负整数,且存在一整数0∈G有0+a=a+0=a,所以(1)为融洽集;
(3)当a,b 都为平面向量时,两平面向量相加任然为平面向量,且存在0向量通过向量加法满足条件②
(2),(4)中找不到满足条件②的e,
∴答案为(1),(3).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 关于运算
关于运算 满足:(1)对任意
满足:(1)对任意 、
、 ,都有
,都有 ;(2)存在
;(2)存在 ,使得对一切
,使得对一切 ,都有
,都有 ,则称
,则称 {非负整数},
{非负整数},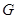 关于运算
关于运算 满足:(1)对任意
满足:(1)对任意 、
、 ,都有
,都有 ;(2)存在
;(2)存在 ,使得对一切
,使得对一切 ,都有
,都有 ,则称
,则称 {非负整数},
{非负整数},