题目内容
4．求函数y=lg（x2+x-6）的单调增区间是（ ）| A． | $（-∞，-\frac{1}{2}）$ | B． | $（-\frac{1}{2}，+∞）$ | C． | （2，+∞） | D． | （-∞，-3） |
分析 令t=x2+x-6＞0，求得函数的定义域为{x|x＜-3，或x＞2}，且 y=lgt，本题即求函数t在定义域为{x|x＜-3，或x＞2}内的增区间．再利用二次函数的性质可得函数t在定义域内的增区间．
解答 解：令t=x2+x-6＞0，求得x＜-3，或x＞2，故函数的定义域为{x|x＜-3，或x＞2}，且 y=lgt，
故本题即求函数t在定义域为{x|x＜-3，或x＞2}内的增区间．
再利用二次函数的性质可得函数t在定义域为{x|x＜-3，或x＞2}内的增区间 （2，+∞），
故选：C．
点评 本题主要考查复合函数的单调性，对数函数、二次函数的性质，体现了转化的数学思想，属于中档题．
练习册系列答案
一线名师提优试卷系列答案
相关题目
15．
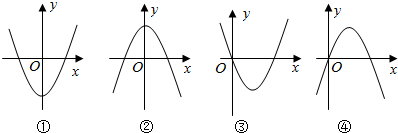下面四个图象中，有一个是函数f（x）=$\frac{1}{3}$x3+ax2+（a2-1）x+1（a∈R）的导函数y=f′（x）的图象，则f（-1）=（ ）
下面四个图象中，有一个是函数f（x）=$\frac{1}{3}$x3+ax2+（a2-1）x+1（a∈R）的导函数y=f′（x）的图象，则f（-1）=（ ）| A． | $\frac{5}{3}$或$-\frac{1}{3}$ | B． | $\frac{5}{3}$或$\frac{1}{3}$ | C． | $-\frac{1}{3}$或$-\frac{5}{3}$ | D． | $\frac{1}{3}$或$-\frac{5}{3}$ |
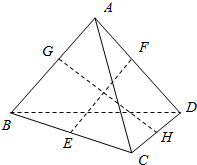已知：正四面体ABCD（所有棱长均相等）的棱长为1，E、F、G、H分别是四面体ABCD中各棱的中点，设：$\overrightarrow{AB}=\overrightarrow a，\overrightarrow{AC}=\overrightarrow b，\overrightarrow{AD}=\overrightarrow c$，试采用向量法解决下列问题
19．已知倾斜角为α的直线l与直线x+2y-3=0垂直，则cos（$\frac{2015π}{2}$-2α）的值为（ ）
| A． | $\frac{4}{5}$ | B． | -$\frac{4}{5}$ | C． | 2 | D． | -$\frac{1}{2}$ |