题目内容
已知函数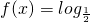 [x2-2(2a-1)x+8](a∈R)
[x2-2(2a-1)x+8](a∈R)
(1)若使函数f(x)在[a,+∞﹚上为减函数,求a的取值范围;
(2)当a= 时,求y=f(
时,求y=f( ),x∈[
),x∈[ ]的值域.
]的值域.
(3)若关于x的方程f(x)=-1+ 在[1,3]上有且只有一解,求a的取值范围.
在[1,3]上有且只有一解,求a的取值范围.
解:(1)∵函数f(x)在[a,+∞﹚上为减函数,
∴
∴ ;
;
(2)当a= 时,
时,
∴y=f( )=
)= ,
,
∵x∈[ ],∴
],∴ ≤
≤ ≤
≤ ,∴-
,∴- ≤sin(
≤sin( )≤1
)≤1
∴函数的值域为[ ];
];
(3)原方可化为x2-2(2a-1)x+8=2x+6>0,
即 ,x∈[1,3],由双勾图形可知:
,x∈[1,3],由双勾图形可知: 或4a=
或4a= ,
,
即 或a=
或a= .
.
分析:(1)利用函数f(x)在[a,+∞﹚上为减函数,建立不等式组,即可求a的取值范围;
(2)确定y=f( ),结合三角函数、对数函数的性质,即可求函数的值域;
),结合三角函数、对数函数的性质,即可求函数的值域;
(3)原方可化为x2-2(2a-1)x+8=2x+6>0,即 ,x∈[1,3],根据在[1,3]上有且只有一解,即可得出结论.
,x∈[1,3],根据在[1,3]上有且只有一解,即可得出结论.
点评:本题考查函数的单调性,函数的值域,考查学生分析解决问题的能力,属于中档题.
∴

∴
 ;
;(2)当a=
 时,
时,
∴y=f(
 )=
)= ,
,∵x∈[
 ],∴
],∴ ≤
≤ ≤
≤ ,∴-
,∴- ≤sin(
≤sin( )≤1
)≤1∴函数的值域为[
 ];
];(3)原方可化为x2-2(2a-1)x+8=2x+6>0,
即
 ,x∈[1,3],由双勾图形可知:
,x∈[1,3],由双勾图形可知: 或4a=
或4a= ,
,即
 或a=
或a= .
.分析:(1)利用函数f(x)在[a,+∞﹚上为减函数,建立不等式组,即可求a的取值范围;
(2)确定y=f(
 ),结合三角函数、对数函数的性质,即可求函数的值域;
),结合三角函数、对数函数的性质,即可求函数的值域;(3)原方可化为x2-2(2a-1)x+8=2x+6>0,即
 ,x∈[1,3],根据在[1,3]上有且只有一解,即可得出结论.
,x∈[1,3],根据在[1,3]上有且只有一解,即可得出结论.点评:本题考查函数的单调性,函数的值域,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
 [x2-2(2a-1)x+8](a∈R)
[x2-2(2a-1)x+8](a∈R) 时,求y=f(
时,求y=f( ),x∈[
),x∈[ ]的值域.
]的值域. 在[1,3]上有且只有一解,求a的取值范围.
在[1,3]上有且只有一解,求a的取值范围.