题目内容
设过点M(-1,0)的直线与椭圆x2+3y2=a2(a>0)相交于A,B两个不同的点,且 =2
=2 .记O为坐标原点.求△OAB的面积取得最大值时的椭圆方程.
.记O为坐标原点.求△OAB的面积取得最大值时的椭圆方程.
【答案】分析:设A(x1,y1),B(x2,y2).利用根与系数的关系及向量相等得到y1,y2的关系及可用k来表示,再利用三角形的面积公式,从而得△OAB的面积 S= |OC|•|y2-y1|及基本不等式的性质,即可得出取得面积最大值时的k的值,进而得到a的值.
|OC|•|y2-y1|及基本不等式的性质,即可得出取得面积最大值时的k的值,进而得到a的值.
解答:证明:由y=k(x+1)(k≠0)得x= y-1.
y-1.
并代入椭圆方程x2+3y2=a2消去x得(3+k2)y2-6ky+3k2-k2a2=0 ①
设A(x1,y1),B(x2,y2).
由①,得y1+y2= ,②
,②
∵ =2
=2 .而点M(-1,0),
.而点M(-1,0),
∴(-1-x1,-y1)=2(x2+1,y2),
得y1=-2y2代入②,得y2= ,③
,③
∴△OAB的面积 S= |OC|•|y2-y1|=
|OC|•|y2-y1|= |y2|=
|y2|= ≤
≤ =
= ,
,
当且仅当k2=3,即k=± 时取等号.
时取等号.
把k的值代人③可得y2=± ,这两组值分别代入①,均可解出a2=15.
,这两组值分别代入①,均可解出a2=15.
∴△OAB的面积取得最大值的椭圆方程是x2+3y2=15.
点评:本小题主要考查直线与圆锥曲线的综合问题、基本不等式、椭圆方程等基础知识,考查运算求解能力、化归与转化思想.属于中档题.
 |OC|•|y2-y1|及基本不等式的性质,即可得出取得面积最大值时的k的值,进而得到a的值.
|OC|•|y2-y1|及基本不等式的性质,即可得出取得面积最大值时的k的值,进而得到a的值.解答:证明:由y=k(x+1)(k≠0)得x=
 y-1.
y-1.并代入椭圆方程x2+3y2=a2消去x得(3+k2)y2-6ky+3k2-k2a2=0 ①
设A(x1,y1),B(x2,y2).
由①,得y1+y2=
 ,②
,②∵
 =2
=2 .而点M(-1,0),
.而点M(-1,0),∴(-1-x1,-y1)=2(x2+1,y2),
得y1=-2y2代入②,得y2=
 ,③
,③∴△OAB的面积 S=
 |OC|•|y2-y1|=
|OC|•|y2-y1|= |y2|=
|y2|= ≤
≤ =
= ,
,当且仅当k2=3,即k=±
 时取等号.
时取等号.把k的值代人③可得y2=±
 ,这两组值分别代入①,均可解出a2=15.
,这两组值分别代入①,均可解出a2=15.∴△OAB的面积取得最大值的椭圆方程是x2+3y2=15.
点评:本小题主要考查直线与圆锥曲线的综合问题、基本不等式、椭圆方程等基础知识,考查运算求解能力、化归与转化思想.属于中档题.

练习册系列答案
相关题目
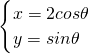 (θ为参数),若A、B是曲线C上关于坐标轴不对称的任意两点.
(θ为参数),若A、B是曲线C上关于坐标轴不对称的任意两点.