题目内容
1.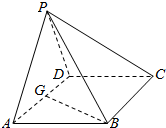 如图,在四棱锥P-ABCD中,底面ABCD是∠DAB=60°且边长为a的菱形,侧面PAD是等边三角形,且平面PAD⊥底面ABD,G为AD的中点,则点G到平面PAB的距离为( )
如图,在四棱锥P-ABCD中,底面ABCD是∠DAB=60°且边长为a的菱形,侧面PAD是等边三角形,且平面PAD⊥底面ABD,G为AD的中点,则点G到平面PAB的距离为( )| A. | $\frac{{\sqrt{15}}}{10}a$ | B. | $\sqrt{5}a$ | C. | $\frac{{\sqrt{5}}}{5}a$ | D. | $\sqrt{15}a$ |
分析 运用等积法通过vG-PAB=VA-PGB,即可求h的值.
解答 解;在四棱锥P-ABCD中,底面ABCD是∠DAB=60°且边长为a的菱形,侧面PAD是等边三角形,
且平面PAD⊥底面ABD,G为AD的中点,可知PG⊥底面ABCD,
设点G到平面PAB的距离为h,△PAB中,PA=AB=a
∴面积S=$\frac{1}{2}$•$\frac{\sqrt{6}}{2}$a•$\sqrt{1-\frac{6}{16}}$a=$\frac{\sqrt{15}}{8}$a2,
∵vG-PAB=VA-PGB=$\frac{1}{3}$×$\frac{\sqrt{15}}{8}$a2×h=$\frac{1}{3}$×$\frac{\sqrt{3}}{8}$a2×$\frac{\sqrt{3}}{2}$a,
∴h=$\frac{\sqrt{15}}{10}a$.
故选:A.
点评 本题考查了空间直线平面的垂直问题,距离问题,运用运用等积法得出空间距离,属于中档题.

练习册系列答案
相关题目
10.${∫}_{0}^{1}$(2x+6x2)dx=( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
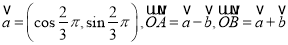 ,若
,若 是以
是以 为直角顶点的等腰直角三角形,则
为直角顶点的等腰直角三角形,则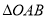 的面积等于( )
的面积等于( ) C.2 D.
C.2 D.
 ,若存在
,若存在 ,使得
,使得 ,则
,则 的取值范围是( )
的取值范围是( ) B.
B.
 D.
D.
 在
在 上单调递增,则
上单调递增,则 与
与 的大小关系是( )
的大小关系是( ) B.
B.
 D.不能确定
D.不能确定