题目内容
已知函数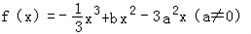
在x=a处取得极值．
（Ⅰ）求
；
（Ⅱ）设函数g（x）=2x3﹣3af′（x）﹣6a3，如果g（x）在开区间（0，1）上存在极小值，求实数a的取值范围．
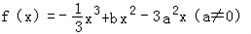在x=a处取得极值．（Ⅰ）求
；（Ⅱ）设函数g（x）=2x3﹣3af′（x）﹣6a3，如果g（x）在开区间（0，1）上存在极小值，求实数a的取值范围．
解（1）f'（x）=﹣x2+2bx﹣3a2
由题意知f'（a）=﹣a2+2ba﹣3a2=0
则b=2a
∴
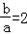
（2）由已知可得g（x）=2x3+3ax2﹣12a2x+3a3
则g'（x）=6x2+6ax﹣12a2=6（x﹣a）（x+2a）
令g'（x）=0，得x=a或x=﹣2a
若a＞0，当x＜﹣2a或x＞a时，g'（x）＞0；
当﹣2a＜x＜a时，g'（x）＜0
所以当x=a时，g（x）有极小值，
∴0＜a＜1若a＜0，
当x＜a或x＞﹣2a时，g'（x）＞0；
当a＜x＜﹣2a时，g'（x）＜0
所以当x=﹣2a时，g（x）有极小值，
∴0＜﹣2a＜1即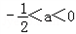
所以当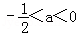
或0＜a＜1时，g（x）在开区间（0，1）上存在极小值．
由题意知f'（a）=﹣a2+2ba﹣3a2=0
则b=2a
∴
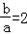
（2）由已知可得g（x）=2x3+3ax2﹣12a2x+3a3
则g'（x）=6x2+6ax﹣12a2=6（x﹣a）（x+2a）
令g'（x）=0，得x=a或x=﹣2a
若a＞0，当x＜﹣2a或x＞a时，g'（x）＞0；
当﹣2a＜x＜a时，g'（x）＜0
所以当x=a时，g（x）有极小值，
∴0＜a＜1若a＜0，
当x＜a或x＞﹣2a时，g'（x）＞0；
当a＜x＜﹣2a时，g'（x）＜0
所以当x=﹣2a时，g（x）有极小值，
∴0＜﹣2a＜1即
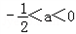
所以当
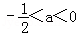或0＜a＜1时，g（x）在开区间（0，1）上存在极小值．
练习册系列答案
寒假乐园北京教育出版社系列答案
相关题目
在x=1处取到极值 
时，给定定义域为D=［0,1］时，函数
是否满足对任意的
都有
.如果是，请给出证明；如果不是，请说明理由. 
在x=1处取到极值 
时，给定定义域为D=［0,1］时，函数
是否满足对任意的
都有
.如果是，请给出证明；如果不是，请说明理由. 
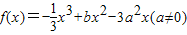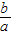在x=a处取得极值．
；
在x=a处取得极值．
；
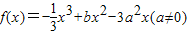在x=a处取得极值．
；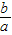