题目内容
已知函数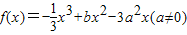 在x=a处取得极值.
在x=a处取得极值.(Ⅰ)求
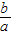 ;
;(Ⅱ)设函数g(x)=2x3-3af′(x)-6a3,如果g(x)在开区间(0,1)上存在极小值,求实数a的取值范围.
【答案】分析:(1)先求导函数,然后根据导数的几何意义可知f'(a)=0,可求出 的值;
的值;
(2)将b用a表示,可求出函数g(x)的解析式,讨论a的正负,分别求出函数的极值点,使极值点在开区间(0,1)上,建立不等式关系,解之即可.
解答:解(1)f'(x)=-x2+2bx-3a2
由题意知f'(a)=-a2+2ba-3a2=0则b=2a
∴
(2)由已知可得g(x)=2x3+3ax2-12a2x+3a3
则g'(x)=6x2+6ax-12a2=6(x-a)(x+2a)
令g'(x)=0,得x=a或x=-2a
若a>0,当x<-2a或x>a时,g'(x)>0;
当-2a<x<a时,g'(x)<0
所以当x=a时,g(x)有极小值,
∴0<a<1
若a<0,当x<a或x>-2a时,g'(x)>0;
当a<x<-2a时,g'(x)<0
所以当x=-2a时,g(x)有极小值,
∴0<-2a<1即
所以当 或0<a<1时,g(x)在开区间(0,1)上存在极小值.
或0<a<1时,g(x)在开区间(0,1)上存在极小值.
点评:本题主要考查了函数在某点取得极值的条件,以及利用导数法求极值,同时考查了分类讨论的思想和运算求解的能力,属于中档题.
 的值;
的值;(2)将b用a表示,可求出函数g(x)的解析式,讨论a的正负,分别求出函数的极值点,使极值点在开区间(0,1)上,建立不等式关系,解之即可.
解答:解(1)f'(x)=-x2+2bx-3a2
由题意知f'(a)=-a2+2ba-3a2=0则b=2a
∴

(2)由已知可得g(x)=2x3+3ax2-12a2x+3a3
则g'(x)=6x2+6ax-12a2=6(x-a)(x+2a)
令g'(x)=0,得x=a或x=-2a
若a>0,当x<-2a或x>a时,g'(x)>0;
当-2a<x<a时,g'(x)<0
所以当x=a时,g(x)有极小值,
∴0<a<1
若a<0,当x<a或x>-2a时,g'(x)>0;
当a<x<-2a时,g'(x)<0
所以当x=-2a时,g(x)有极小值,
∴0<-2a<1即

所以当
 或0<a<1时,g(x)在开区间(0,1)上存在极小值.
或0<a<1时,g(x)在开区间(0,1)上存在极小值.点评:本题主要考查了函数在某点取得极值的条件,以及利用导数法求极值,同时考查了分类讨论的思想和运算求解的能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 在x=a处取得极值.
在x=a处取得极值. ;
;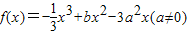 在x=a处取得极值.
在x=a处取得极值.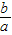 ;
;