题目内容
17.设z1=1+i,复数z1,z2在复平面内的对应点关于实轴对称,则$\frac{z_1}{z_2}$=( )| A. | i | B. | -i | C. | -1 | D. | 1 |
分析 由已知求得复数z2,代入$\frac{z_1}{z_2}$,利用复数代数形式的乘除运算化简得答案.
解答 解:∵z1=1+i,且复数z1,z2在复平面内的对应点关于实轴对称,
∴z2=1-i,
则$\frac{z_1}{z_2}$=$\frac{1+i}{1-i}=\frac{(1+i)^{2}}{(1-i)(1+i)}=\frac{2i}{2}=i$.
故选:A.
点评 本题考查复数代数形式的乘除运算,是基础的计算题.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
5.已知定义在R上函数y=f(x+1)是偶函数,且在[0,+∞)上单调,若数列{an}是公差不为0的等差数列,且f(a6)=f(a20),则{an}的前25项之和为( )
| A. | 0 | B. | $\frac{25}{2}$ | C. | 25 | D. | 50 |
9.已知α,β,γ为不同的平面,l,m为不同的直线.若α∩β=l,m?α,l∥γ,m⊥γ.则( )
| A. | m∥β | B. | m⊥β | C. | l∥m | D. | l⊥m |
6.某地一家课外培训机构随机选取当地1000名学生的数据,研究他们报名参加数学、英语、物理、化学培训的情况,整理成如下统计表:
表中“√”表示参加,“×”表示未参加.
(1)估计当地某一学生同时参加英语和物理培训的概率;
(2)估计当地某一学生在以上四门课程同时参加三门培训的概率;
(3)如果一个学生参加了数学培训,则该生同时参加英语、物理、化学培训中哪一种的可能性最大?说明理由.
| 课程 人数 | 数学 | 英语 | 物理 | 化学 |
| 100 | √ | × | √ | √ |
| 217 | × | √ | × | √ |
| 200 | √ | √ | √ | × |
| 300 | √ | × | √ | × |
| 85 | √ | × | × | × |
| 98 | × | √ | × | × |
(1)估计当地某一学生同时参加英语和物理培训的概率;
(2)估计当地某一学生在以上四门课程同时参加三门培训的概率;
(3)如果一个学生参加了数学培训,则该生同时参加英语、物理、化学培训中哪一种的可能性最大?说明理由.
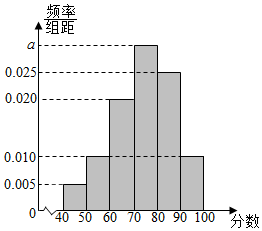 某校从高二年级学生中随机抽取40名学生,将他们的期中考试政治成绩(满分100分,成绩均不低于40分的整数)分成六段:[40,50),[50,60),[60,70),[70,80)[80,90),[90,100]后,得到如图所示的频率分布直方图.
某校从高二年级学生中随机抽取40名学生,将他们的期中考试政治成绩(满分100分,成绩均不低于40分的整数)分成六段:[40,50),[50,60),[60,70),[70,80)[80,90),[90,100]后,得到如图所示的频率分布直方图.