题目内容
当点P在曲线y=sinx（x∈（0，π））上移动时，曲线在P处切线的倾斜角的取值范围是
- A.
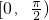
- B.
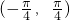
- C.
- D.
∪
D
分析：先求出y′，然后设直线的倾斜角为α，则tanα=y′，然后根据x的范围得到y′的范围即tanα的范围，根据正切函数的图象及增减性得到α的范围即可．
解答：
解：设该切线的倾斜角为α，则tanα=y′=cosx，
因为x∈（0，π），所以cosx∈（-1，1）
根据直线倾斜角的范围为（0，π）和正切函数的图象及单点区间，
利用图象可得：α∈[0，
）∪（
，π）
故选D
点评：此题考查学生会利用数形结合求直线的倾斜角，会求正切函数的值域，会求函数的导函数，做题时利用数形结合的数学思想解决实际问题．
分析：先求出y′，然后设直线的倾斜角为α，则tanα=y′，然后根据x的范围得到y′的范围即tanα的范围，根据正切函数的图象及增减性得到α的范围即可．
解答：
解：设该切线的倾斜角为α，则tanα=y′=cosx，因为x∈（0，π），所以cosx∈（-1，1）
根据直线倾斜角的范围为（0，π）和正切函数的图象及单点区间，
利用图象可得：α∈[0，
）∪（，π）故选D
点评：此题考查学生会利用数形结合求直线的倾斜角，会求正切函数的值域，会求函数的导函数，做题时利用数形结合的数学思想解决实际问题．
练习册系列答案
相关题目
当点P在曲线y=sinx（x∈（0，π））上移动时，曲线在P处切线的倾斜角的取值范围是（ ）
A、[0，
| ||||
B、(-
| ||||
C、(
| ||||
D、[0，
|
)处切线的斜率k；
t4-3,求当t=5时物体运动的瞬时速率v.
∪