题目内容
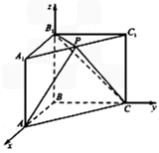
如图,在直三棱柱ABC﹣A1B1C1中,AB⊥BC,P为A1C1的中点,AB=BC=kPA.
(I)当k=1时,求证PA⊥B1C;
(II)当k为何值时,直线PA与平面BB1C1C所成的角的正弦值为 ,并求此时二面角A﹣PC﹣B的余弦值.
,并求此时二面角A﹣PC﹣B的余弦值.
(I)当k=1时,求证PA⊥B1C;
(II)当k为何值时,直线PA与平面BB1C1C所成的角的正弦值为
 ,并求此时二面角A﹣PC﹣B的余弦值.
,并求此时二面角A﹣PC﹣B的余弦值. 
解:以点B为坐标原点,分别以直线BA、BC、BB1为x轴、y轴建立空间直角坐标系Oxyz.(I)设AB=2,则AB=BC=PA=2
根据题意得: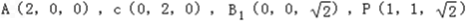
所以 .
.
∵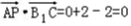 ,∴PA⊥B1C.
,∴PA⊥B1C.
(II)设AB=2,则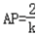 ,
,
根据题意:A(2,0,0),C(0,2,0),
又因为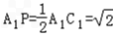 ,
,
所以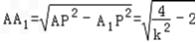 ,
,
∴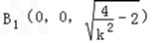 ,
,
∴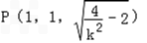
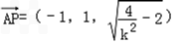 ,
,
∵AB⊥平面B1C,
所以由题意得 ,即
,即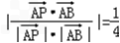 ,即
,即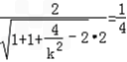 ,
,
∵k>0,解得k= .
.
即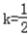 时,直线PA与平面BB1C1C所成的角的正弦值为
时,直线PA与平面BB1C1C所成的角的正弦值为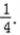
∵B1P⊥面APC,∴平面APC的法向量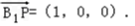
设平面BPC的一个法向量为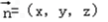 ,
,
∵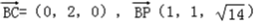 由
由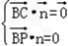 ,得
,得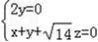 , ∴
, ∴ 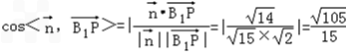
所以此时二面角A﹣PC﹣B的余弦值是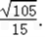
根据题意得:
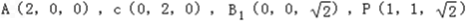
所以
 .
.∵
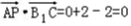 ,∴PA⊥B1C.
,∴PA⊥B1C.(II)设AB=2,则
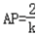 ,
,根据题意:A(2,0,0),C(0,2,0),
又因为
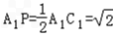 ,
,所以
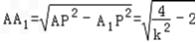 ,
, ∴
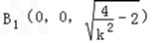 ,
, ∴
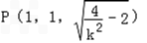
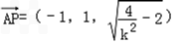 ,
,∵AB⊥平面B1C,
所以由题意得
 ,即
,即 ,即
,即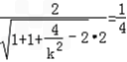 ,
,∵k>0,解得k=
 .
.即
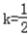 时,直线PA与平面BB1C1C所成的角的正弦值为
时,直线PA与平面BB1C1C所成的角的正弦值为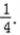
∵B1P⊥面APC,∴平面APC的法向量
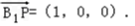
设平面BPC的一个法向量为
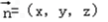 ,
,∵
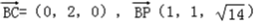 由
由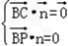 ,得
,得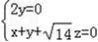 , ∴
, ∴ 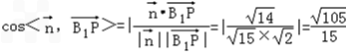
所以此时二面角A﹣PC﹣B的余弦值是
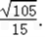

练习册系列答案
相关题目




