题目内容
已知椭圆C: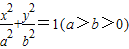 的长轴长为4,F1,F2分别为其左、右焦点,抛物线y2=-4x的焦点为F1.
的长轴长为4,F1,F2分别为其左、右焦点,抛物线y2=-4x的焦点为F1.(Ⅰ)求椭圆C的方程;
(Ⅱ)过焦点F1的直线l与椭圆C交于P,Q两点,求△F2PQ面积的最大值.
【答案】分析:(Ⅰ)抛物线y2=4x的焦点为(1,0)即c=1,再利用椭圆定义,求出2a,得出a,可求得椭圆C的方程;
(II)设直线l方程为:x=my-1,将直线的方程代入椭圆的方程,消去x得到关于y的一元二次方程,再结合根系数的关系利用弦长公式即可求得△F2PQ面积值,最后利用求函数的最大值,从而解决问题.
解答:解:(Ⅰ)由抛物线y2=-4x的焦点为F1(-1,0)可知c=1,
∵2a=4∴a=2,∴b2=a2-c2=3
所以椭圆C的方程为: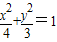 …(4分)
…(4分)
(Ⅱ)因为过点F1(-1,0)的直线与椭圆C交于P,Q两点,
可设直线l方程为:x=my-1,P(x1,y1),Q(x2,y2),则
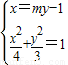 ,得(4+3m2)y2-6my-9=0,∴
,得(4+3m2)y2-6my-9=0,∴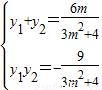
所以S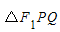 =
= |F1F2||y1-y2|=
|F1F2||y1-y2|=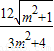 ,
,
令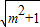 =t,则t≥1,所以S
=t,则t≥1,所以S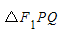 =
=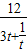
而3t+ 在[1,+∞)上单调递增,
在[1,+∞)上单调递增,
所以S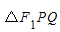 =
=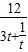 ≤3,当t=1时取等号,
≤3,当t=1时取等号,
即当m=0时,△F2PQ的面积最大值为3…(8分)
点评:本题考查圆锥曲线定义、标准方程、简单的几何性质.属于直线与圆锥曲线的综合问题.
(II)设直线l方程为:x=my-1,将直线的方程代入椭圆的方程,消去x得到关于y的一元二次方程,再结合根系数的关系利用弦长公式即可求得△F2PQ面积值,最后利用求函数的最大值,从而解决问题.
解答:解:(Ⅰ)由抛物线y2=-4x的焦点为F1(-1,0)可知c=1,
∵2a=4∴a=2,∴b2=a2-c2=3
所以椭圆C的方程为:
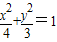 …(4分)
…(4分)(Ⅱ)因为过点F1(-1,0)的直线与椭圆C交于P,Q两点,
可设直线l方程为:x=my-1,P(x1,y1),Q(x2,y2),则
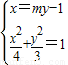 ,得(4+3m2)y2-6my-9=0,∴
,得(4+3m2)y2-6my-9=0,∴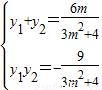
所以S
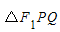 =
= |F1F2||y1-y2|=
|F1F2||y1-y2|=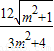 ,
,令
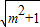 =t,则t≥1,所以S
=t,则t≥1,所以S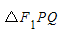 =
=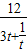
而3t+
 在[1,+∞)上单调递增,
在[1,+∞)上单调递增,所以S
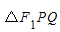 =
=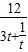 ≤3,当t=1时取等号,
≤3,当t=1时取等号,即当m=0时,△F2PQ的面积最大值为3…(8分)
点评:本题考查圆锥曲线定义、标准方程、简单的几何性质.属于直线与圆锥曲线的综合问题.

练习册系列答案
相关题目
 的长轴长为4.
的长轴长为4. 相切,求椭圆焦点坐标;
相切,求椭圆焦点坐标; ,求椭圆的方程.
,求椭圆的方程. 已知椭圆C:
已知椭圆C: 的长轴长是短轴长的
的长轴长是短轴长的 倍,F1,F2是它的左,右焦点.
倍,F1,F2是它的左,右焦点. ,|PF1|•|PF2|=4,求椭圆C的方程;
,|PF1|•|PF2|=4,求椭圆C的方程; |QM|,,求动点Q的轨迹方程.
|QM|,,求动点Q的轨迹方程. 的长轴长为
的长轴长为 ,离心率
,离心率 .
. ,求直线l的方程.
,求直线l的方程.
 的长轴长为
的长轴长为 ,离心率
,离心率 .
. ,求直线l的方程.
,求直线l的方程.
 的长轴长是短轴长的
的长轴长是短轴长的 倍,F1,F2是它的左,右焦点.
倍,F1,F2是它的左,右焦点. ,|PF1|•|PF2|=4,求椭圆C的方程;
,|PF1|•|PF2|=4,求椭圆C的方程; |QM|,,求动点Q的轨迹方程.
|QM|,,求动点Q的轨迹方程.