题目内容
11.函数$y={log_{\frac{1}{3}}}(-3+4x-{x^2})$的单调递增区间是[2,3).分析 令t=-3+4x-x2>0,求得函数的定义域,结合y=${log}_{\frac{1}{3}}t$,本题即求函数t在(1,3)上的减区间,再利用二次函数的性质可得结论.
解答 解:令t=-3+4x-x2>0,求得1<x<3,则y=${log}_{\frac{1}{3}}t$,
本题即求函数t在(1,3)上的减区间.
利用二次函数的性质可得函数t在(1,3)上的减区间为[2,3),
故答案为:[2,3).
点评 本题主要考查复合函数的单调性,二次函数的性质,体现了转化的数学思想,属于中档题.

练习册系列答案
相关题目
6.若三角形三边长之比是1:$\sqrt{3}$:2,则其所对角之比是( )
| A. | 1:2:3 | B. | 1:$\sqrt{3}$:2 | C. | 1:$\sqrt{2}$:$\sqrt{3}$ | D. | $\sqrt{2}$:$\sqrt{3}$:2 |
16.下列函数中,既是偶函数又在(0,+∞)上单调递增的是( )
| A. | y=x3 | B. | y=ln|x| | C. | y=-x2 | D. | y=2x |
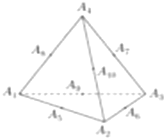 已知正四面体A1A2A3A4,点A5,A6,A7,A8,A9,A10分别是所在棱的中点,如图,则当1≤i≤10,1≤j≤10,且i≠j时,数量积$\overrightarrow{{A}_{1}{A}_{2}}•\overrightarrow{{A}_{i}{A}_{j}}$的不同数值的个数为9.
已知正四面体A1A2A3A4,点A5,A6,A7,A8,A9,A10分别是所在棱的中点,如图,则当1≤i≤10,1≤j≤10,且i≠j时,数量积$\overrightarrow{{A}_{1}{A}_{2}}•\overrightarrow{{A}_{i}{A}_{j}}$的不同数值的个数为9.