题目内容
求证:空间四边形相邻两边中点的连线平行于经过另外两边所在的平面.
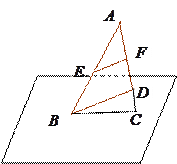
已知:如图,空间四边形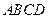 中,
中,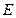 ,
,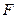 分别是
分别是 ,
,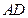 的中点.
的中点.
 求证:
求证: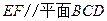
已知:如图,空间四边形
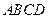 中,
中,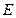 ,
,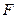 分别是
分别是 ,
,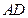 的中点.
的中点. 求证:
求证: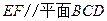
证明过程见解析
连接 ,
,
因为 ,
, ,
,
所以 (三角形中位线的性质).
(三角形中位线的性质).
因为 ,
, ,
,
由直线与平面平行的判定定理得 .
.
 ,
,因为
 ,
, ,
,所以
 (三角形中位线的性质).
(三角形中位线的性质).因为
 ,
, ,
,由直线与平面平行的判定定理得
 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
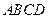 中,
中,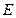 ,
,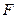 分别是
分别是 ,
,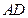 的中点.
的中点. 求证:
求证: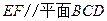
 ,
, ,
, ,
, (三角形中位线的性质).
(三角形中位线的性质). ,
, ,
, .
.
 阅读快车系列答案
阅读快车系列答案