题目内容
存在整数n,使
+
是整数的质数p( )
| p+n |
| n |
分析:设
=a,
=b(a,b是整数),再平方相减,利用平方差公式可得结论.
| p+n |
| n |
解答:解:设
=a,
=b(a,b是整数),则p=a2-b2=(a+b)(a-b)
若p是质数,只需满足a+b=p,a-b=1,显然满足条件的p有无数个
故选D.
| p+n |
| n |
若p是质数,只需满足a+b=p,a-b=1,显然满足条件的p有无数个
故选D.
点评:本题考查演绎推理,考查学生分析解决问题的能力,属于基础题.

练习册系列答案
相关题目
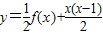 的反函数为p(x),t(x)=p(x)(1-x),求函数t(x)的最大值;
的反函数为p(x),t(x)=p(x)(1-x),求函数t(x)的最大值;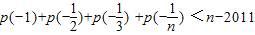 恒成立?若存在,请找出一个满足条件的N的值,并给以说明;若不存在,请说明理由.
恒成立?若存在,请找出一个满足条件的N的值,并给以说明;若不存在,请说明理由.