题目内容
不等式x2-2mx-1＞0对一切1≤x≤3都成立，求m的取值范围.
思路分析：只需{x|1≤x≤3}?{x|x2-2mx-1>0}即可，仍应借助图象列出m应满足的不等式.
解：由题意知x2-2mx-1>0的解集包含集合{x|1≤x≤3},从而方程x2-2mx-1=0的两实根（它们恒存在且不等）x1、x2要么都大于3,要么都小于1.
由于x1·x2=-1，故只能x1、x2都小于1.
作出函数y=x2-2mx-1的图象（满足两根均小于1）的示意图（下图），即知只需x=1时,y＞0即可.
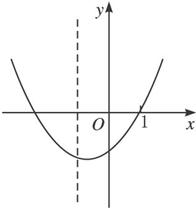
所以12-2m-1＞0.所以m<0.
故m的取值范围是{m|m<0}.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目