题目内容
下列说法不正确的序号是(1)函数y=
| ax-a-x |
| 2 |
(2)函数f(x)=
| (ax+1)x |
| ax-1 |
(3)若f(x)=3x,则f(x+y)=f(x)f(y);
(4)若f(x)=ax(a>0,a≠1),且x1≠x2,则
| 1 |
| 2 |
| x1+x2 |
| 2 |
分析:利用函数奇偶性的定义判断命题(1)(2);利用指数函数的性质及基本不等式判断命题(3)(4)
解答:解:对于(1),令f(x)=y=
将x用-x代替得f(-x)=
=-f(x),为奇函数
对于(2)f(-x)=
=
=f(x),为偶函数
对于(3)f(x+y)=3x+y,f(x)f(y)=3x•3y=3x+y,有f(x+y)=f(x)f(y);
对于(4)
[f(x1)+f(x2)]=
(ax1+ax2),≥f(
)=a
故答案为(4)
| ax-a-x |
| 2 |
| a-x-ax |
| 2 |
对于(2)f(-x)=
| (a-x+1)(-x) |
| a-x-1 |
| (ax+1)x |
| ax-1 |
对于(3)f(x+y)=3x+y,f(x)f(y)=3x•3y=3x+y,有f(x+y)=f(x)f(y);
对于(4)
| 1 |
| 2 |
| 1 |
| 2 |
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
故答案为(4)
点评:本题考查利用函数奇偶性的定义判断函数的鸡偶性、指数函数的性质.

练习册系列答案
相关题目
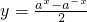 (a>0,a≠1)是奇函数;
(a>0,a≠1)是奇函数;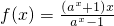 (a>0,a≠1)是偶函数;
(a>0,a≠1)是偶函数;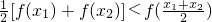 .
. (a>0,a≠1)是奇函数;
(a>0,a≠1)是奇函数; (a>0,a≠1)是偶函数;
(a>0,a≠1)是偶函数; .
.