题目内容
对每个正整数n,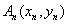 是抛物线
是抛物线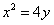 上的点,过焦点F的直线FAn,交抛物线于另一点
上的点,过焦点F的直线FAn,交抛物线于另一点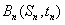 。
。
(1)试证: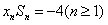 ;
;
(2)取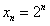 ,并
,并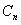 为抛物线上分别为
为抛物线上分别为 与
与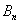 为切点的两条切线的交点,求证
为切点的两条切线的交点,求证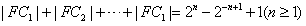 。
。
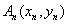 是抛物线
是抛物线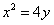 上的点,过焦点F的直线FAn,交抛物线于另一点
上的点,过焦点F的直线FAn,交抛物线于另一点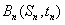 。
。(1)试证:
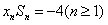 ;
;(2)取
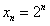 ,并
,并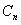 为抛物线上分别为
为抛物线上分别为 与
与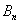 为切点的两条切线的交点,求证
为切点的两条切线的交点,求证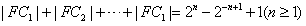 。
。 证明:(1)焦点为(0,1),
设直线AnBn的方程为: ,
,
联立 ,消去y,得
,消去y,得
 ,
,
∴ 。
。
(2)由 ,则
,则 ,
,
∴ 在An处的切线方程为
在An处的切线方程为 ,
,
即 , ①
, ①
同理:在Bn处切线方程为: , ②
, ②
两式相减,得 ,
,
代入(1)中结论,得y=-1,
∴ ,
,
∴ ,
,
即 ,
,
∴
 。
。
设直线AnBn的方程为:
 ,
,联立
 ,消去y,得
,消去y,得 ,
,∴
 。
。(2)由
 ,则
,则 ,
,∴
 在An处的切线方程为
在An处的切线方程为 ,
,即
 , ①
, ①同理:在Bn处切线方程为:
 , ②
, ②两式相减,得
 ,
,代入(1)中结论,得y=-1,
∴
 ,
,∴
 ,
,即
 ,
,∴

 。
。
练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
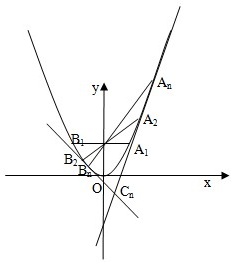 如图,对每个正整数n,An(xn,yn)是抛物线x2=4y上的点,过焦点F的直线FAn交抛物线于另一点Bn(sn,tn).
如图,对每个正整数n,An(xn,yn)是抛物线x2=4y上的点,过焦点F的直线FAn交抛物线于另一点Bn(sn,tn). 是抛物线
是抛物线 上的点,过焦点F的直线FAn交抛物线另一点
上的点,过焦点F的直线FAn交抛物线另一点 。
。
 并
并 为抛物线上分别为
为抛物线上分别为 与
与 为切点的两条切线的交点,求证
为切点的两条切线的交点,求证
