题目内容
过(2,2)点且与曲线x2+y2+2x-2y-2=0相交所得弦长为2
的直线方程为( )
| 3 |
分析:曲线x2+y2+2x-2y-2=0化为标准方程,确定圆心与半径,设出直线方程,利用条件可得圆心到直线的距离为1,从而可求直线方程.
解答:解:曲线x2+y2+2x-2y-2=0化为标准方程为:(x+1)2+y-1)2=4,表示圆心为(-1,1),半径为2的圆
设过点(2,2)的直线方程为y-2=k(x-2),即kx-y-2k+2=0
∵过(2,2)点且与曲线x2+y2+2x-2y-2=0相交所得弦长为2
∴圆心到直线的距离为
=1
∴
=1
∴4k2+3k=0
∴k=0,或k=-
∴所求直线方程为:3x-4y+2=0或y=2
故选C.
设过点(2,2)的直线方程为y-2=k(x-2),即kx-y-2k+2=0
∵过(2,2)点且与曲线x2+y2+2x-2y-2=0相交所得弦长为2
| 3 |
∴圆心到直线的距离为
| 4-3 |
∴
| |-3k+1| | ||
|
∴4k2+3k=0
∴k=0,或k=-
| 3 |
| 4 |
∴所求直线方程为:3x-4y+2=0或y=2
故选C.
点评:本题重点考查直线与圆的位置关系,考查点到直线距离公式的运用,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
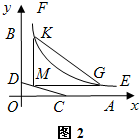
 如图1,OA,OB是某地一个湖泊的两条互相垂直的湖堤,线段CD和曲线段EF分别是湖泊中的一座栈桥和一条防波堤.为观光旅游的需要,拟过栈桥CD上某点M分别修建与OA,OB平行的栈桥MG、MK,且以MG、MK为边建一个跨越水面的三角形观光平台MGK.建立如图2所示的直角坐标系,测得线段CD的方程是x+2y=20(0≤x≤20),曲线段EF的方程是xy=200(5≤x≤40),设点M的坐标为(s,t),记z=s•t.(题中所涉及的长度单位均为米,栈桥和防波堤都不计宽度
如图1,OA,OB是某地一个湖泊的两条互相垂直的湖堤,线段CD和曲线段EF分别是湖泊中的一座栈桥和一条防波堤.为观光旅游的需要,拟过栈桥CD上某点M分别修建与OA,OB平行的栈桥MG、MK,且以MG、MK为边建一个跨越水面的三角形观光平台MGK.建立如图2所示的直角坐标系,测得线段CD的方程是x+2y=20(0≤x≤20),曲线段EF的方程是xy=200(5≤x≤40),设点M的坐标为(s,t),记z=s•t.(题中所涉及的长度单位均为米,栈桥和防波堤都不计宽度