题目内容
下列从集合A到集合B的对应中是映射的是
[ ]
A．
A＝B＝N＋，对应法则f：x→y＝|x－3|
B．
A＝R，B＝{0，1}，对应法则f：x→y＝
C．
A＝B＝R，对应法则f：x→y＝±
D．
A＝Z，B＝Q，对应法则f：x→y＝
答案：B
解析：
解析：
|
在A中，当x＝3时，|x－3|＝0，于是A中有一个元素3在B中没有元素和它对应，故不是映射．C显然不是映射．在D中，集合A中的元素0，其倒数不存在，因而B中也无元素与它对应，故同样不是映射．B符合映射的定义，故选B．判断两个集合A、B之间的对应是否为映射，只要依照对应法则f判断：对于A中任何一个元素，在B中是否有惟一的元素和它对应． |
练习册系列答案
王后雄学案教材完全解读系列答案
相关题目
下列从集合A到集合B的对应f是映射的是（ ）
A、 | B、 | C、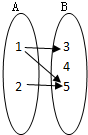 | D、 |
在下列从集合
A到集合B的对应关系中，不可以确定y是x的函数的是[
]①
A={x|xÎZ|，B= {y|yÎZ}，对应法则
；
②
A={x|x＞0|，B= {y|yÎR}，对应法则f：x®
=2x；
③
A={x|xÎR|，B= {y|yÎR}，对应法则f：x®y=
；
|
A ．① |
B ．② |
C ．③ |
D ．①②③ |
；
=2x；
；
