题目内容
已知Sn是数列{an}的前n项和,Sn满足关系式 ,
, (n≥2,n为正整数).
(n≥2,n为正整数).
(1)令bn=2nan,求证数列{bn}是等差数列,
(2)求数列{an}的通项公式;
(3)对于数列{un},若存在常数M>0,对任意的n∈N*,恒有|un+1-un|+|un-un-1|+…|u2-u1|≤M成立,称数列{un}为“差绝对和有界数列”,证明:数列{an}为“差绝对和有界数列”;
解:(1)当n≥2时,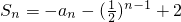 ,
,
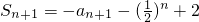
所以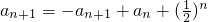 ,
,
即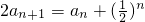 ,
,
所以2n+1an+1=2n•an+1
即bn+1-bn=1,(n≥2),又b2-b1=22•2×a1=1
所以,bn+1-bn=1,n∈N+即{bn}为等差数列
(2)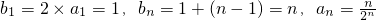
(3)由于|an+1-an|+|an-an-1|+…+|a2-a1|= +
+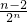 +…+
+…+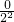
sn- sn<
sn<
所以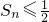 恒成立,
恒成立,
即[an]为“差绝对和有界数列”.
分析:(1)整理题设递推式得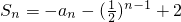 进而表示出Sn+1,进而根据an+1=Sn+1-Sn,求得an+1和an的递推式,整理得2n+1an+1=2n•an+1,进而根据bn=2nan,求得bn+1-bn=1,进而根据等差数列的定义判断出数列为等差数列.
进而表示出Sn+1,进而根据an+1=Sn+1-Sn,求得an+1和an的递推式,整理得2n+1an+1=2n•an+1,进而根据bn=2nan,求得bn+1-bn=1,进而根据等差数列的定义判断出数列为等差数列.
(2)根据(1)中数列{bn}的首项和公差,求得数列的通项公式,进而根据bn=2nan求得an.
(3)把an代入|an+1-an|+|an-an-1|+…+|a2-a1|中,利用利用错位想减法求得sn- sn<
sn< ,进而判断出以
,进而判断出以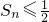 恒成立,根据“差绝对和有界数列”的定义,证明出数列{an}为“差绝对和有界数列”.
恒成立,根据“差绝对和有界数列”的定义,证明出数列{an}为“差绝对和有界数列”.
点评:本题主要考查了数列的递推式.考查了学生综合分析问题和创造性思维的能力.
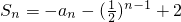 ,
,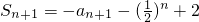
所以
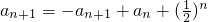 ,
,即
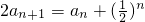 ,
,所以2n+1an+1=2n•an+1
即bn+1-bn=1,(n≥2),又b2-b1=22•2×a1=1
所以,bn+1-bn=1,n∈N+即{bn}为等差数列
(2)
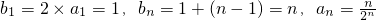
(3)由于|an+1-an|+|an-an-1|+…+|a2-a1|=
 +
+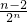 +…+
+…+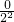
sn-
 sn<
sn<
所以
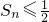 恒成立,
恒成立,即[an]为“差绝对和有界数列”.
分析:(1)整理题设递推式得
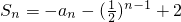 进而表示出Sn+1,进而根据an+1=Sn+1-Sn,求得an+1和an的递推式,整理得2n+1an+1=2n•an+1,进而根据bn=2nan,求得bn+1-bn=1,进而根据等差数列的定义判断出数列为等差数列.
进而表示出Sn+1,进而根据an+1=Sn+1-Sn,求得an+1和an的递推式,整理得2n+1an+1=2n•an+1,进而根据bn=2nan,求得bn+1-bn=1,进而根据等差数列的定义判断出数列为等差数列.(2)根据(1)中数列{bn}的首项和公差,求得数列的通项公式,进而根据bn=2nan求得an.
(3)把an代入|an+1-an|+|an-an-1|+…+|a2-a1|中,利用利用错位想减法求得sn-
 sn<
sn< ,进而判断出以
,进而判断出以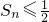 恒成立,根据“差绝对和有界数列”的定义,证明出数列{an}为“差绝对和有界数列”.
恒成立,根据“差绝对和有界数列”的定义,证明出数列{an}为“差绝对和有界数列”.点评:本题主要考查了数列的递推式.考查了学生综合分析问题和创造性思维的能力.

练习册系列答案
相关题目