题目内容
函数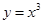 在
在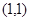 处的切线与
处的切线与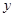 轴交点的纵坐标为( )
轴交点的纵坐标为( )
A. | B. | C.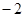 | D. |
C
解析试题分析:因为 ,根据导数的几何意义可知函数
,根据导数的几何意义可知函数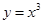 在
在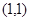 处的切线的斜率为
处的切线的斜率为 ,所以该切线方程为
,所以该切线方程为 即
即 ,所以该切线与
,所以该切线与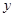 轴交点的纵坐标为该直线的纵截距
轴交点的纵坐标为该直线的纵截距 ,故选C.
,故选C.
考点:导数的几何意义.

练习册系列答案
相关题目
设函数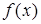 在R上可导,其导函数为
在R上可导,其导函数为 且函数
且函数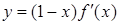 的图像如图所示,则下列结论一定成立的是( )
的图像如图所示,则下列结论一定成立的是( )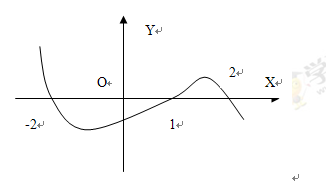
A.函数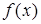 的极大值是 的极大值是 ,极小值是 ,极小值是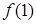 |
B.函数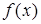 的极大值是 的极大值是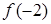 ,极小值是 ,极小值是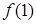 |
C.函数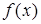 的极大值是 的极大值是 ,极小值是 ,极小值是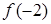 |
D.函数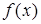 的极大值是 的极大值是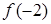 ,极小值是 ,极小值是 |
若曲线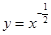 在点
在点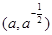 处的切线与两坐标轴围成的三角形面积为18.则
处的切线与两坐标轴围成的三角形面积为18.则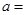 ( )
( )
| A.64 | B.32 | C.16 | D.8 |
定义域为R的函数f(x)满足f(1)=1,且f(x)的导函数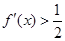 ,则满足
,则满足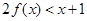 的x的集合为( )
的x的集合为( )
| A.{x|x<1} | B.{x|-1<x<1} | C.{x|x<-1或x>1} | D.{x|x>1} |
设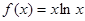 ,若
,若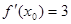 ,则
,则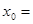 ( )
( )
A.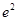 | B.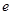 | C.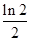 | D.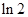 |
函数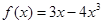 (
( )的最大值是( )
)的最大值是( )
A.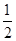 | B.-1 | C.0 | D.1 |
[2013·浙江高考]已知e为自然对数的底数,设函数f(x)=(ex-1)(x-1)k(k=1,2),则( )
| A.当k=1时,f(x)在x=1处取到极小值 |
| B.当k=1时,f(x)在x=1处取到极大值 |
| C.当k=2时,f(x)在x=1处取到极小值 |
| D.当k=2时,f(x)在x=1处取到极大值 |
函数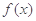 是
是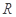 上的可导函数,
上的可导函数, 时,
时, ,则函数
,则函数 的零点个数为( )
的零点个数为( )
A. | B. | C. | D. |
如图所示,在边长为1的正方形OABC中任取一点P,则点P恰好取自阴影部分的概率为( )
A. | B. |
C. | D. |