题目内容
()选修4-1:几何证明讲![]()
![]()
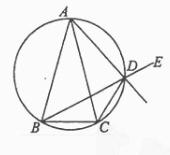 已知
已知 ![]() ABC 中,AB=AC, D是
ABC 中,AB=AC, D是 ![]() ABC外接圆劣弧
ABC外接圆劣弧![]() 上的点(不与点A,C重合),延长BD至E。
上的点(不与点A,C重合),延长BD至E。
(1) 求证:AD的延长线平分![]() CDE;
CDE;
(2) 若![]() BAC=30,
BAC=30,![]() ABC中BC边上的高为2+
ABC中BC边上的高为2+![]() ,求
,求![]() ABC外接圆的面积。
ABC外接圆的面积。![]()
![]()
(I)略(II)4![]()
解析:
(Ⅰ)如图,设F为AD延长线上一点
 ∵A,B,C,D四点共圆,
∵A,B,C,D四点共圆,
∴∠CDF=∠ABC
又AB=AC ∴∠ABC=∠ACB,
且∠ADB=∠ACB, ∴∠ADB=∠CDF,
对顶角∠EDF=∠ADB, 故∠EDF=∠CDF,
即AD的延长线平分∠CDE.
(Ⅱ)设O为外接圆圆心,连接AO交BC于H,则AH⊥BC.
连接OC,A由题意∠OAC=∠OCA=150, ∠ACB=750,
∴∠OCH=600.
设圆半径为r,则r+![]() r=2+
r=2+![]() ,a得r=2,外接圆的面积为4
,a得r=2,外接圆的面积为4![]() 。
。

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
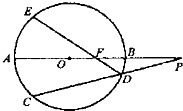 (2013•太原一模)选修4一1:几何证明选讲
(2013•太原一模)选修4一1:几何证明选讲
 选修4一1:几何证明选讲
选修4一1:几何证明选讲
 ,求
,求 的大小.
的大小.
 ,求
,求 的值.
的值.
 如图,已知AP是⊙O的切线,P为切点,AC是⊙O的割线,与⊙O交于B、C两点,圆心O在
如图,已知AP是⊙O的切线,P为切点,AC是⊙O的割线,与⊙O交于B、C两点,圆心O在 的内部,点M是BC的中点.
的内部,点M是BC的中点.