题目内容
已知双曲线C1: 的离心率为2.若抛物线
的离心率为2.若抛物线 的焦点到双曲线C1的渐近线的距离为2,则抛物线C2的方程为( )
的焦点到双曲线C1的渐近线的距离为2,则抛物线C2的方程为( )A.

B.x2=
 y
yC.x2=8y
D.x2=16y
【答案】分析:利用双曲线的离心率推出a,b的关系,求出抛物线的焦点坐标,通过点到直线的距离求出p,即可得到抛物线的方程.
解答:解:双曲线C1: 的离心率为2.
的离心率为2.
所以 ,即:
,即: =4,所以
=4,所以 ;双曲线的渐近线方程为:
;双曲线的渐近线方程为:
抛物线 的焦点(0,
的焦点(0, )到双曲线C1的渐近线的距离为2,
)到双曲线C1的渐近线的距离为2,
所以2= ,因为
,因为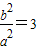 ,所以p=8.
,所以p=8.
抛物线C2的方程为x2=16y.
故选D.
点评:本题考查抛物线的简单性质,点到直线的距离公式,双曲线的简单性质,考查计算能力.
解答:解:双曲线C1:
 的离心率为2.
的离心率为2.所以
 ,即:
,即: =4,所以
=4,所以 ;双曲线的渐近线方程为:
;双曲线的渐近线方程为:
抛物线
 的焦点(0,
的焦点(0, )到双曲线C1的渐近线的距离为2,
)到双曲线C1的渐近线的距离为2,所以2=
 ,因为
,因为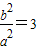 ,所以p=8.
,所以p=8.抛物线C2的方程为x2=16y.
故选D.
点评:本题考查抛物线的简单性质,点到直线的距离公式,双曲线的简单性质,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的离心率为2,若抛物线C2:
的离心率为2,若抛物线C2: 的焦点到双曲线C1的渐近线的距离是2,则抛物线C2的方程是(
)
的焦点到双曲线C1的渐近线的距离是2,则抛物线C2的方程是(
) B.
B.
 D.
D.
 的离心率为2,若抛物线C2:
的离心率为2,若抛物线C2: 的焦点到双曲线C1的渐近线的距离是2,则抛物线C2的方程是
的焦点到双曲线C1的渐近线的距离是2,则抛物线C2的方程是 B.
B.
 D.
D.
 的离心率为2.若抛物线
的离心率为2.若抛物线 的焦点到双曲线C1的渐近线的距离为2,则抛物线C2的方程为( )
的焦点到双曲线C1的渐近线的距离为2,则抛物线C2的方程为( )
 y
y 的离心率为2.若抛物线
的离心率为2.若抛物线 的焦点到双曲线C1的渐近线的距离为2,则抛物线C2的方程为( )
的焦点到双曲线C1的渐近线的距离为2,则抛物线C2的方程为( )
 y
y